Institute Output
What Ultimately Is There? Metaphysics and the Ruliad
Stephen Wolfram
“What ultimately is there?” has always been seen as a fundamental—if thorny—question for philosophy, or perhaps theology. But despite a couple of millennia of discussion, I think it’s fair to say that only modest progress has been made with it. But maybe, just maybe, this is the moment where that’s going to change—and on the basis of surprising new ideas and new results from our latest efforts in science, it’s finally going to be possible to make real progress, and in the end to build what amounts to a formal, scientific approach to metaphysics.
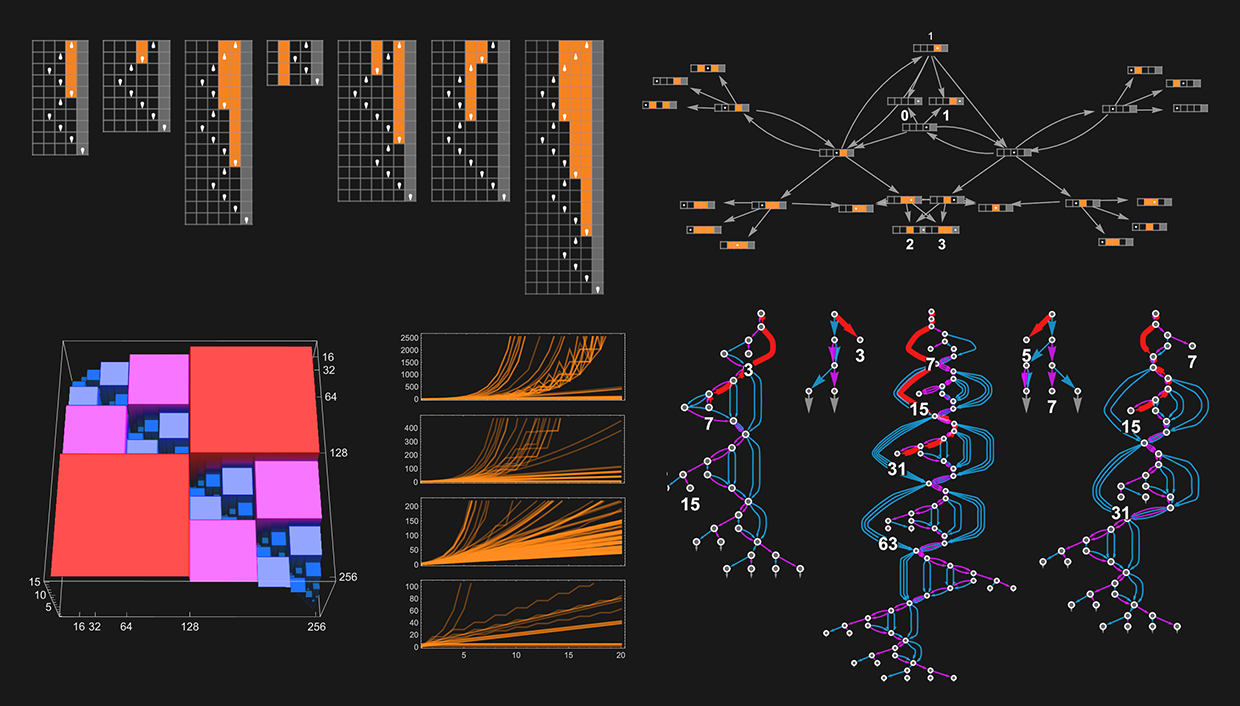
P vs. NP and the Difficulty of Computation: A Ruliological Approach
Stephen Wolfram
“Could there be a faster program for that?” It’s a fundamental type of question in theoretical computer science. But except in special cases, such a question has proved fiendishly difficult to answer. And, for example, in half a century, almost no progress has been made even on the rather coarse (though very famous) P vs. NP question—essentially of whether for any nondeterministic program there will always be a deterministic one that is as fast. From a purely theoretical point of view, it’s never been very clear how to even start addressing such a question. But what if one were to look at the question empirically, say in effect just by enumerating possible programs and explicitly seeing how fast they are, etc.?

Computational Metaphysics: A Survey of the Ruliad, Observer Theory and Emerging Frameworks
James K. Wiles
A concise survey of how recent computational models, such as the ruliad and observer theory, are transforming metaphysical questions into formal, testable frameworks.

On the Concept of Motion
Stephen Wolfram
It seems like the kind of question that might have been hotly debated by ancient philosophers, but would have been settled long ago: how is it that things can move? And indeed with the view of physical space that’s been almost universally adopted for the past two thousand years it’s basically a non-question. As crystallized by the likes of Euclid it’s been assumed that space is ultimately just a kind of “geometrical background” into which any physical thing can be put—and then moved around.
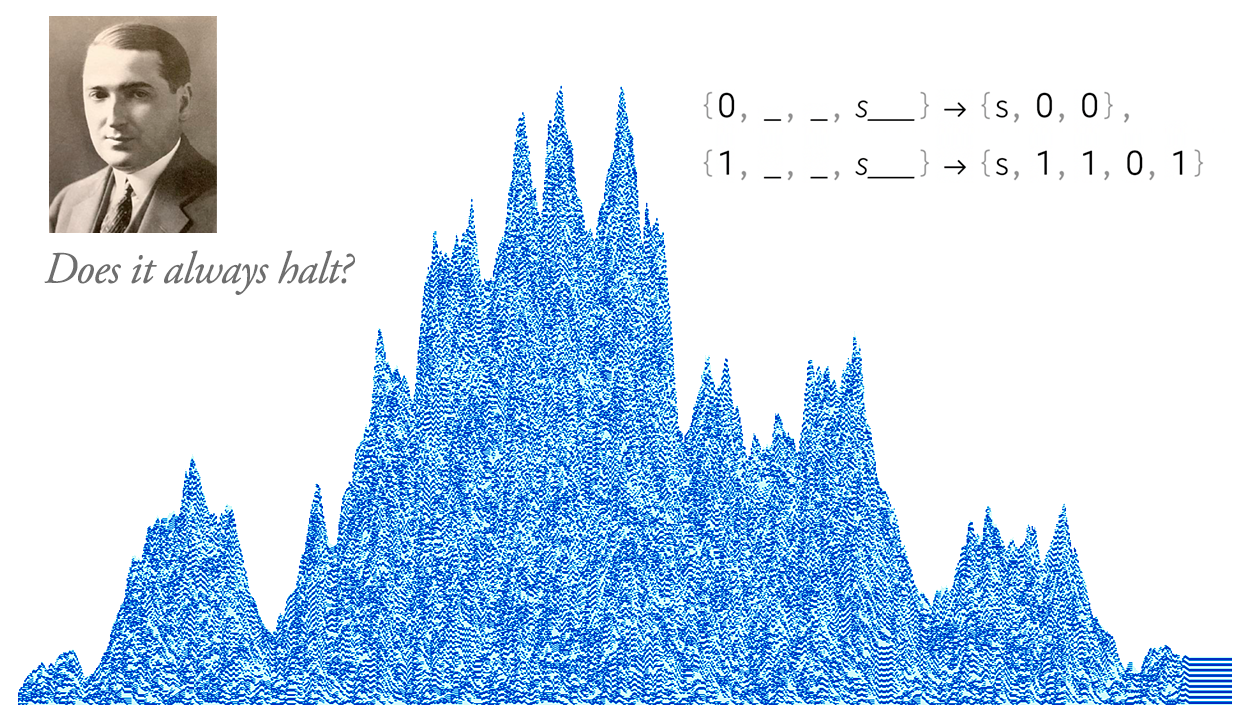
After 100 Years, Can We Finally Crack Post’s Problem of Tag? A Story of Computational Irreducibility, and More
Stephen Wolfram
For Post, the failure to crack his system derailed his whole intellectual worldview. For me now, the failure to crack Post’s system in a sense just bolsters my worldview—providing yet more indication of the strength and ubiquity of computational irreducibility and the Principle of Computational Equivalence.

Exploring Rulial Space: The Case of Turing Machines
Stephen Wolfram
Let’s say we find a rule that reproduces physics. A big question would then be: “Why this rule, and not another?” I think there’s a very elegant potential answer to this question, that uses what we’re calling rule space relativity—and that essentially says that there isn’t just one rule: actually all possible rules are being used, but we’re basically picking a reference frame that makes us attribute what we see to some particular rule. In other words, our description of the universe is a sense of our making, and there can be many other—potentially utterly incoherent—descriptions, etc.
