Institute Output
P vs. NP and the Difficulty of Computation: A Ruliological Approach
Stephen Wolfram
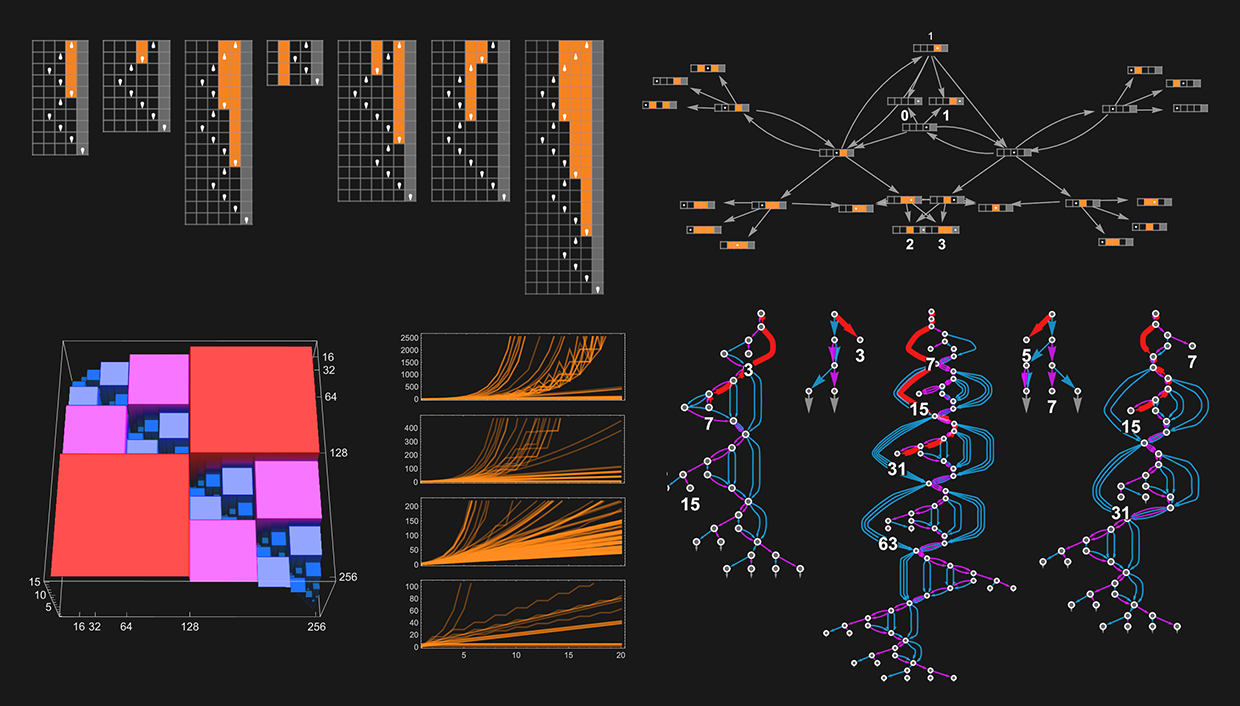
“Could there be a faster program for that?” It’s a fundamental type of question in theoretical computer science. But except in special cases, such a question has proved fiendishly difficult to answer. And, for example, in half a century, almost no progress has been made even on the rather coarse (though very famous) P vs. NP question—essentially of whether for any nondeterministic program there will always be a deterministic one that is as fast. From a purely theoretical point of view, it’s never been very clear how to even start addressing such a question. But what if one were to look at the question empirically, say in effect just by enumerating possible programs and explicitly seeing how fast they are, etc.?
Quantum Operators From Wolfram Model Multiway Systems
Furkan Semih Dündar, Xerxes D. Arsiwalla, Hatem Elshatlawy
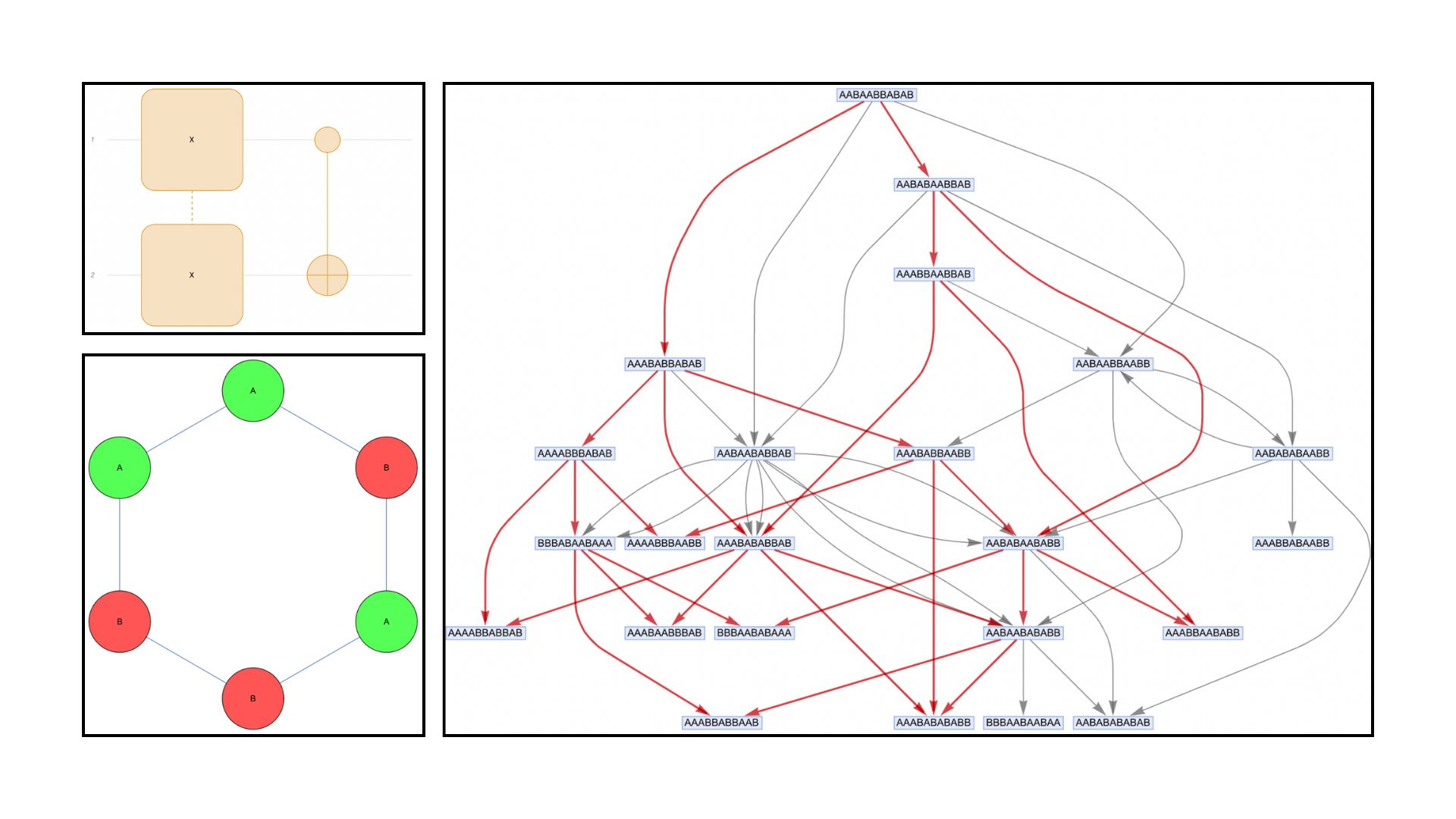
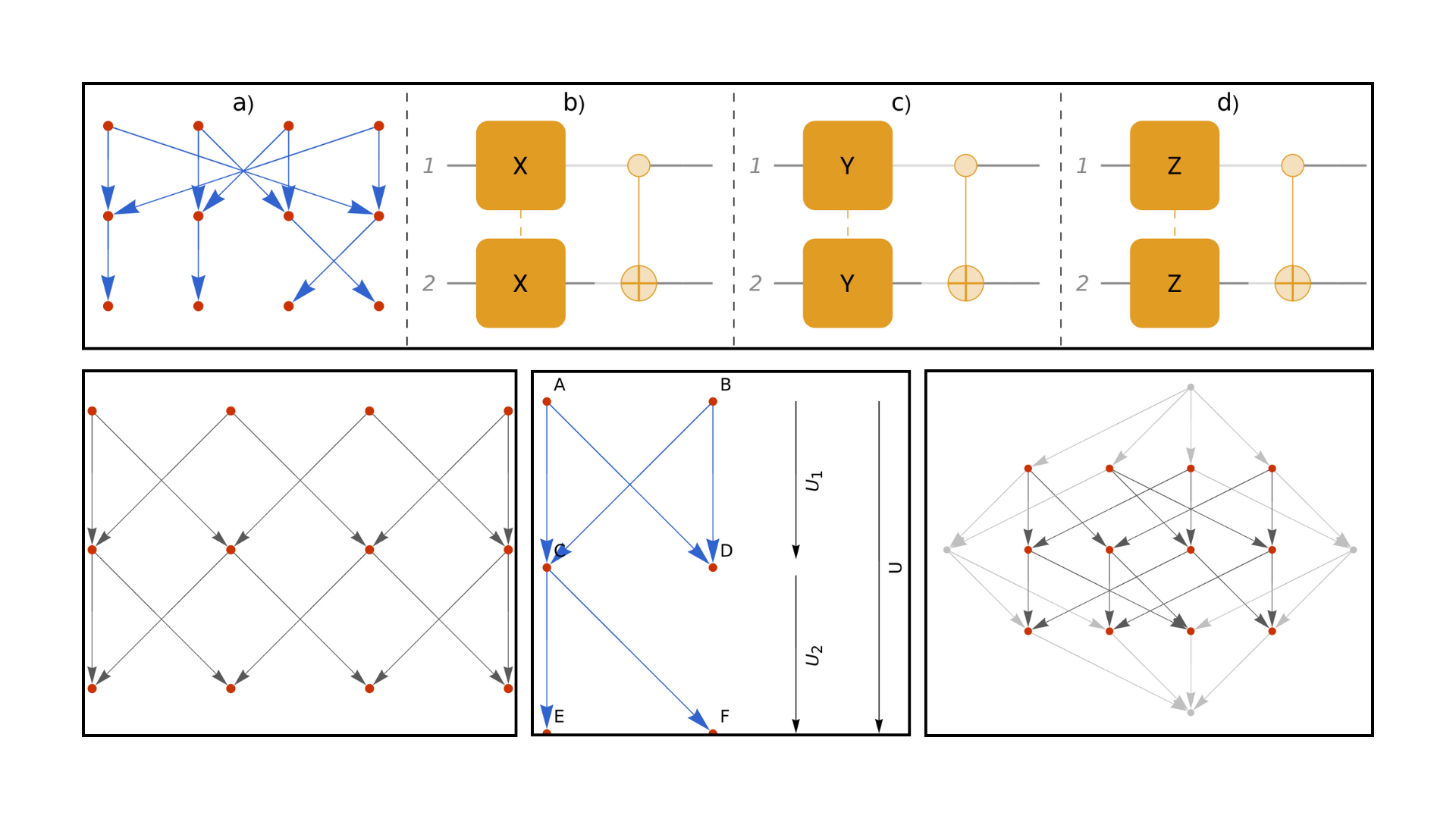
Using Wolfram Model multiway rewriting systems we have found that by using multiway systems one can construct representations of quantum circuits, showing that one can encode the Hadamard gate, the π/8 gate and the CNOT using multiway rewriting systems. This suggests the possibility of universal quantum computation using multiway rewriting.

What Is Ruliology?
Stephen Wolfram
Ruliology is taking off! And more and more people are talking about it. But what is ruliology? Since I invented the term, I decided I should write something to explain it. But then I realized: I actually already wrote something back in 2021 when I first invented the term. What I wrote back then was part of something longer. But here now is the part that explains ruliology.
Quantum Gates from Wolfram Model Multiway Rewriting Systems
Furkan Semih Dündar, Xerxes D. Arsiwalla, Hatem Elshatlawy
We show how representations of finite-dimensional quantum operators can be constructed using nondeterministic rewriting systems. In particular, we investigate Wolfram model multiway rewriting systems based on string substitutions.

What’s Special about Life? Bulk Orchestration and the Rulial Ensemble in Biology and Beyond
Stephen Wolfram
It’s a key feature of living systems, perhaps even in some ways the key feature: that even right down to a molecular scale, things are orchestrated. Molecules (or at least large ones) don’t just move around randomly, like in a liquid or a gel. Instead, what molecular biology has discovered is that there are endless active mechanisms that in effect orchestrate what even individual molecules in living systems do. But what is the result of all that orchestration? And could there perhaps be a general characterization of what happens in systems that exhibit such “bulk orchestration”?

Quantum Gravity and Computation: Information, Pregeometry, and Digital Physics
Dean Rickles, Xerxes D. Arsiwalla, Hatem Elshatlawy
This volume argues that concepts from the theory of computation—including information theory, formal languages, and discrete structures—might provide novel paths towards a solution to the problem of quantum gravity. By combining elements of physics with computer science and mathematics, the volume proposes to transform the foundations of spacetime physics and bring it into the digital age.

Upper Bounds on the Chromatic Index of Linear Hypergraphs
Thomas Murff, Xerxes D. Arsiwalla
This work studies upper bounds on the chromatic index of linear, loopless hypergraphs. The first bound is derived using a color-preserving group acting on a properly and minimally edge-colored hypergraph, where the group’s orbits create a finer partition of the coloring. This provides an upper bound on the chromatic index. The following results examine combinatorial properties of hypergraph coloring and outline a possible approach to the Berge–Füredi conjecture, linking the chromatic index to the maximum degree of the associated graph plus one. Three sufficient conditions are also identified for the conjecture to hold, involving the Helly property for hypergraphs.

The Ruliology of Lambdas
Stephen Wolfram
It’s a story of pure, abstract computation. In fact, historically, one of the very first. But even though it’s something I for one have used in practice for nearly half a century, it’s not something that in all my years of exploring simple computational systems and ruliology I’ve ever specifically studied. And, yes, it involves some fiddly technical details. But it’ll turn out that lambdas—like so many systems I’ve explored—have a rich ruliology, made particularly significant by their connection to practical computing.

Human Language and Machine Language
The explosion of large language models means that we are all suddenly awash in machine-generated language, spoken, written and even sung. There are many advantages to the artificial intelligence produced like this, and many disadvantages too: it remains to be seen what the eventual outcome will be. But there is one particular idea that keeps bubbling up to the surface: that AI is going to decide to kill us all. This, I suggest, is based on a misunderstanding of the nature of language.

“I Have a Theory Too”: The Challenge and Opportunity of Avocational Science
Stephen Wolfram
Most physicists term people who send such theories “crackpots”, and either discard their missives or send back derisive responses. I’ve never felt like that was the right thing to do. Somehow I’ve always felt as if there has to be a way to channel that interest and effort into something that would be constructive and fulfilling for all concerned. And maybe, just maybe, I now have at least one idea in that direction.

Towards a Theory for the Speed of Biological Evolution
Willem Nielsen
An exploration of whether general principles govern the speed of evolution. Modified cellular automata models inspired by Stephen Wolfram are used to examine how genome dimensionality and the number of viable solutions influence rapid evolutionary bursts resembling punctuated equilibrium.
SetReplace
Max Piskunov
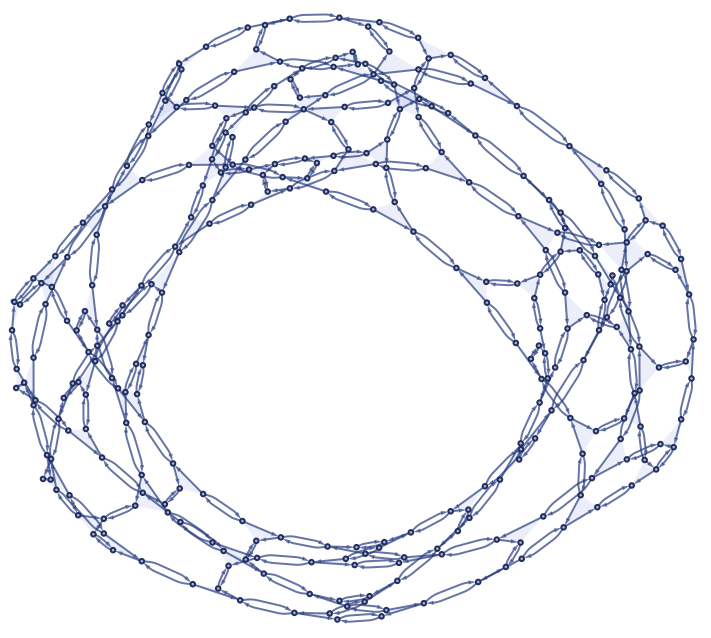
SetReplace is an open‑source Wolfram Language package that executes set‑substitution systems. It evolves user‑defined rules from an initial state and returns structured objects that expose events, causal dependencies, and branching dynamics for analysis and visualization.

Kolmogorov Complexity vs. Computational Irreducibility: Understanding the Distinction
James K. Wiles
Kolmogorov complexity and computational irreducibility describe two kinds of limits on simplification, but they apply in different ways. Kolmogorov complexity measures the shortest possible description of an object, such as a string. Computational irreducibility refers to processes that cannot be predicted or accelerated. This paper introduces each concept, explains their theoretical distinction, and illustrates the difference using simple examples.

Computational Metaphysics: A Survey of the Ruliad, Observer Theory and Emerging Frameworks
James K. Wiles
A concise survey of how recent computational models, such as the ruliad and observer theory, are transforming metaphysical questions into formal, testable frameworks.

What If We Had Bigger Brains? Imagining Minds beyond Ours
Stephen Wolfram
We humans have perhaps 100 billion neurons in our brains. But what if we had many more? Or what if the AIs we built effectively had many more? What kinds of things might then become possible? At 100 billion neurons, we know, for example, that compositional language of the kind we humans use is possible. At the 100 million or so neurons of a cat, it doesn’t seem to be. But what would become possible with 100 trillion neurons? And is it even something we could imagine understanding?

Observer Theory and the Ruliad: An Extension to the Wolfram Model
Sam A. Senchal
This paper introduces a rigorous category-theoretic extension to Observer Theory within Wolfram's Ruliad framework, demonstrating how observers and observes like us sample and integrate information across hierarchical domains, addressing consciousness, causation, and the transition from discrete computational processes to continuous perceived reality.
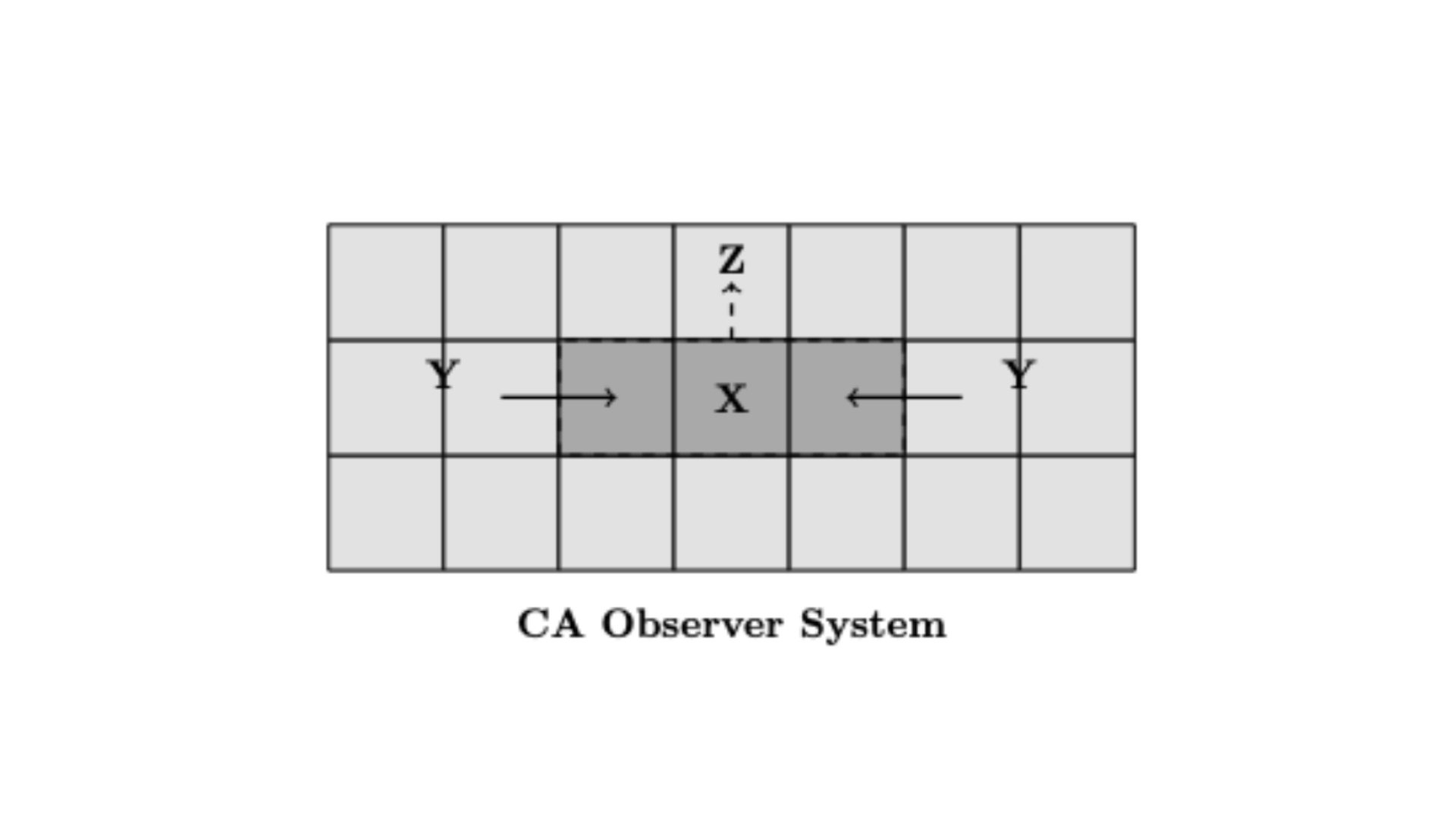
Towards a Generalized Theory of Observers
Hatem Elshatlawy, Xerxes Arsiwalla
A proposal of a formal framework for understanding and unifying the concept of observers across physics, computer science, philosophy, and related fields.

Non-Equilibrium Dynamics of Hard Spheres in the Fluid, Crystalline, and Glassy Regimes
Xerxes D. Arsiwalla, Matthew Kafker
An investigation of the response of a system of hard spheres to two classes of perturbations over a range of densities spanning the fluid, crystalline, and glassy regimes within a molecular dynamics framework.

What Can We Learn about Engineering and Innovation from Half a Century of the Game of Life Cellular Automaton?
Stephen Wolfram
Things are invented. Things are discovered. And somehow there’s an arc of progress that’s formed. But are there what amount to “laws of innovation” that govern that arc of progress?
There are some exponential and other laws that purport to at least measure overall quantitative aspects of progress (number of transistors on a chip; number of papers published in a year; etc.). But what about all the disparate innovations that make up the arc of progress? Do we have a systematic way to study those?

Nature's Compass: A visual exploration of hierarchy in biology and beyond
Willem Nielsen
A discussion of the computational essence of hierarchy in biology and its potential implications for everyday life.
