It took thousands of years of civilized life before the Laws of Physical Motion crystalized. In a way, it makes sense, because when you observe all the different types of motion that occur, it’s not clear that there is any universality. Things move at different speeds, in different directions, with different accelerations, depending on their mass, and the mass of objects around them. But, almost remarkably, there are laws that all these situations follow, first defined in Newton’s Principia.
In biology, we have defined evolution as a powerful and wide-reaching explanation for the different life forms we observe here on earth. However, the speed at which evolution proceeds in different situations, what you could call “The Laws of Biological Motion” are still up in the air. Many biologists will likely say that this is because they do not exist, or that they are too complex to define with simple statements. But, as we saw in physics, it can take a while for laws to show themselves, so I think this is still a worthwhile question to explore.
To find the rates of biological evolution in different situations, I will use the model from Stephen Wolfram’s blog post, with some minor modifications to fit our needs. In Wolfram’s model he defines rules for computational programs as genes, and the results of those programs as the organism. He defines the metric of fitness to be the length at which those automata run (excluding infinite). He defines the evolutionary process to be the search for automata of the same or longer length than the current automata. This works well for modeling how life can go from simple to complex, but for our purposes of observing speed, it’s helpful to get even more minimal.
Genes and organisms are the same, but we will define the evolutionary process as starting from initial automata, and finding new automata of the same length as the initial. The speed of evolution is therefore the rate of discovery of new automata.
Starting with this rule:
Just like Wolfram, we define a point mutation as flipping one of the colors in the rule like so:
We do all possible point mutations starting from the initial rule:
And here is the resulting automata:
We then keep only the ones that run for exactly 11 steps. That is, ones that are the same length as the original:
Now we simply recurse, getting all the mutations for our newly selected automata, and from those selecting the automata of length 11:
And we can continue this process. Going one more step and only showing the selected automata:
Almost all of these have the exact same “phenotype”. So we can simplify by only showing different phenotypes. Here is that same graph, phenotypically reduced:
Pretty underwhelming, and when I was exploring this space, I didn’t expect to get anything much more interesting than this. But let’s search a bit deeper and see what happens. Here we show going 6 steps deep:
Things are moving a bit faster, not only are we discovering more automata, but they are looking very different from each other and from our initial one. Going 9 steps deep we get:
Again, we’re moving faster, with many new “ideas”. At 11 steps we get:
So we’re seeing a large speedup in the discovery process. To give you a sense for the rate of discovery, here we show the discoveries made in each of the first 6 steps:
And here are the discoveries of the last 4 steps:
And in a way, this makes sense, because we’re searching a 26-dimensional space, so as we go deeper we’re searching a lot more nodes. Here’s a graph showing the number of nodes searched:
And here’s the graph of new automaton discovered, or what we defined as the speed of evolution:
Are we expanding into phenotype space?
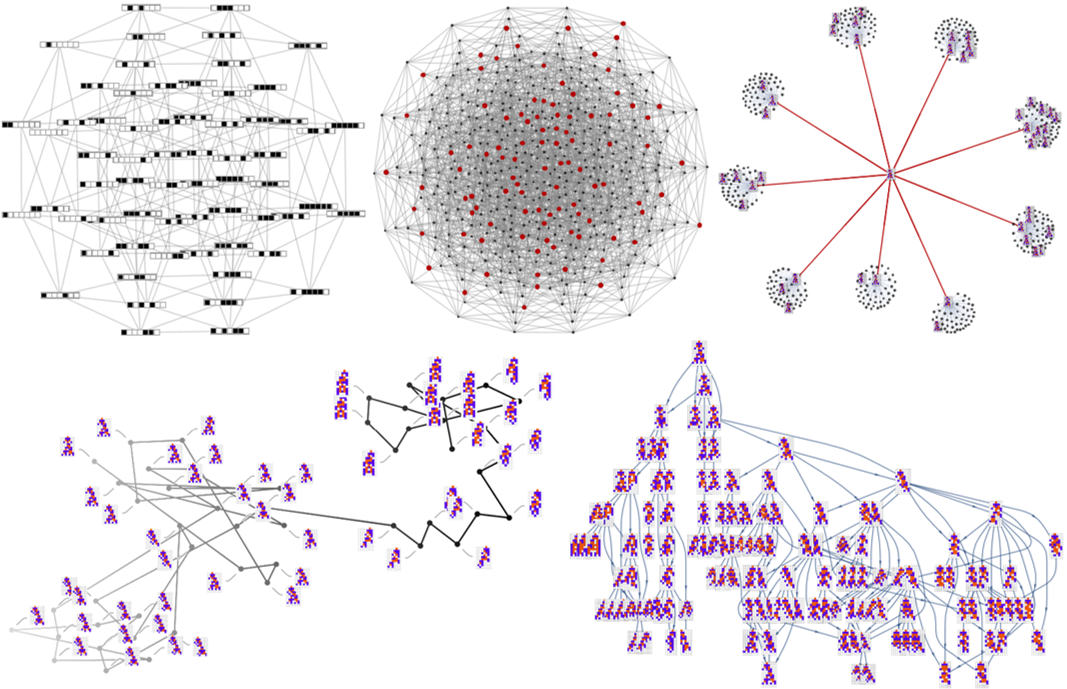
One question here is, “Are we just getting more ‘species’ or are we actually getting more diversity”. In other words, are we moving inwards, getting a more and more detailed graph? Or are we actually expanding out into phenotype space? And if you look at the progressive phenotype graphs below, it’s not clear whether we’re actually expanding our graph in phenotype space.
To answer this we can graph all our automata in feature space, and progressively add the automata at each step. If the automata appear to spread out, then we know they’re actually breaking new ground.
Here are all the automata in feature space:
And here is all the automata as we search deeper and deeper:
So it appears that it is expanding into feature space, although not at every step. For instance, the jump between 8 and 9 gives a huge expansion, but between 9 and 10 we mostly move inward.
Here we plot the area of each region.
Overall takeaway
So our first takeaway is the following: When you have a high dimensional genome space, and you search in many different directions (or you could think of this as allowing many different phenotypes to exist at once), then you can get a rapid increase in the rate of evolution, like the one we saw above. This is a simple, but powerful idea. When biological evolution is taught, it is usually taught as if it is one process, as if it has the same properties, whether acting on viruses in Wuhan, rats in Manhattan, lions in the Bronx Zoo, or hamsters in your cousin’s basement. While there is some truth to this, it gives the misguided impression that evolution should have a single speed. In fact, when Darwin conceived of evolution, he assumed it must be a gradual process, because it was seemingly impossible to explain the complex designs otherwise. But Darwin turned out to be wrong about this. In the 70’s, spurred by a reexamination of tiny animal fossils in The Burgess Shale, a new theory emerged. Biologists realized that many of the fossils in the shale were not part of any group known today, as they originally thought. The time period came to be known as “The Cambrian Explosion”. The theory, stating that rapid evolution occurs in short time windows, followed by long stretches of very little change, is called “Punctuated Equilibrium”. And with our example above, we saw how our model agrees with that theory.
So evolution clearly doesn’t have a single speed. But is there still some general law governing it’s motion? Well in the above example we gotten an important hint, namely, that the dimensionality of genome space increases the rate of evolution. But can we say something precise about how exactly dimensionality and any other important factors affect the rate of evolution? To do this, it’s helpful to further simplify the model.
Zooming in on genome space
We’ll now ignore the organism and just focus on the genes. Here we show a very small genome space of 5-bits:
Now instead of looking for automata of a constant length, we will just randomly define a set of genes to be “fit”. Here we randomly choose 10 genes to be fit:
So how can evolution move through the “fitness space”? Here’s the subgraph containing only the fit genotypes:
Things start to get interesting when you increase the size of genome. Here’s a 7-bit genome space:
Taking a random fitness sample we get:
And here is the fitness space:
Now we’re starting to get to a level of dimensionality that could produce an explosion of new ideas like we saw above. Let’s keep increasing the size of the genome space, here’s a 10-bit genome with a random fitness set of size 250:
The fitness space now looks like:
Shown in a different way:
With this graph you can clearly see the outward explosions in diversity that we saw in our example above with the 2-color automata. So we’re seeing that even in a 10-bit genome, if you have multiple organisms and search in multiple directions at once, then explosions can happen.
One thing I didn’t mention, is how large I’m making the fitness set. And indeed, even with a 10-bit genome, if the fitness set is small, evolution won’t be able to expand quickly. Here we show what happens if our fitness set is only 100 out of 512 genes:
And here’s our fitness space:
Here we don’t see nearly as much branching as before, so the speed of evolution will be quite slow. So, we’ve seen two critical factors in the rate of evolution. First, you need to have a genome that is high dimensional. Second, you need enough solutions. But just how high-dimensional? And just how many solutions?
We can look at what happens in the 8-bit case as we add more solutions to get a sense for this:
We can see that increasing the number of solutions rapidly increases the connectivity. What if we hold the proportion of solutions constant and increase the dimensionality? Here we show the progression if we keep the solutions to 30% and add dimensions. Again a rapid increase in connectivity:
We are starting to get a feel for how evolution can move in different situations. We;ll now zoom in and look at how a single “species” can evolve over time.
Looking at the speed of single organism evolution
So in his article Wolfram mainly focuses on the programs go from short to long and therefore, from simple to complex. In an attempt to model bacterial resistance, I examined another dimension, that of diversity. One approach is to start with a rule and then explicitly look for “new ideas”. That is, look for automata with the pattern that is most different from any of its predecessors, judged by difference in corresponding boxes.
So we start with this rule here.
Then we generate a bunch of random mutations and select only ones that are about the same length. Of those, we select the one that is most different from the previous automata. In this case, this was the most different. There is a few yellow boxes on the bottom left that are added.
We do this recursively and basically ask the question, how different can we get? And somewhat remarkably, this simple procedure is able to continuously find new automata of similar length.
The way in which this happens varies greatly. In this cases we basically had one radical idea.
In this case we get stuck.
In this case, we have an explosion of new ideas.
And we can see that each time we go in a different direction. This shows us that the space of automata is very rich. So how far can this process go? Here is a run after 30 steps:
Notice how there are new ideas continuously discovered
We can see that process continues to be able to find new solutions. To quantify how the automata change over time, we can look at the number of boxes that are different from the initial automata.
One take away here, is the “pace of innovation” seems to jump around a lot. Also, there is a rapid increase at the start followed by a plateauing effect. This is because the automata can only become so different from the initial. But, if we instead use a feature space plot we can get a better sense of the rate of innovation. Here is that same run with the line darkening over time.
And if we look at the speed of innovation in feature space over time we don’t see the slowdown from before. Here we just take the distances of each step in the plot above.
And the thing to observe here is while there are large fluctuations, the overall rate of innovation stays pretty much constant, which we will see later is not always the case. So we’ve been looking at k = 4, r = 1 automata, does this work with k = 3?
So we can see that it still works, let’s go further with a run of 50 steps.
If you look carefully you can see that the 2-color automata tend to get stuck on one idea for longer. This is because there is simply less solutions. Interestingly, when it does make a jump though, the jump is usually huge. This can be seen in the graph of the differences of each automata with the initial automata.
Notice how it has a big jump to 30, and then has a stretch where it is alternating between two of the same idea:
We never saw something like this with the three color. Now, it’s an interesting question: “How does evolution vary with each generation?”. Does biological evolution prefer many small changes or a few large ones? I think this an interesting question to pursue; Empirically, it seems that it prefers very small changes and non-random ones. Like the shape of human bodies for example. There is clearly some purposeful distribution of height, weight and dimensions, but you very rarely see someone randomly grow a third leg. Evolution is conservative in this way. I think there is something very deep here related to risk-taking principles that all surviving systems must follow, and I’m going to explore that extensively in a different article.
But okay, let’s look at the feature space plot of the 2-color automata to get a better sense of what’s going on.
Again, we can see that change is less continuous, with a bunch of bouncing around in one place followed by a large jump into a new area. Looking at the “derivative of diversity” below we see a similar theme, with much larger jumps than before:
We can also note that while the rate fluctuates greatly between individual steps, the overall rate seems to be staying convex, something we’ll see does not hold when we add multiple organisms.
CITE THIS NOTEBOOK
Towards a theory for the speed of biological evolution
by Willem Nielsen
Wolfram Community, STAFF PICKS, November 13, 2024
https://community.wolfram.com/groups/-/m/t/3319760