Institute Output

Quantum Gates from Wolfram Model Multiway Rewriting Systems
Furkan Semih Dündar, Xerxes D. Arsiwalla, Hatem Elshatlawy
We show how representations of finite-dimensional quantum operators can be constructed using nondeterministic rewriting systems. In particular, we investigate Wolfram model multiway rewriting systems based on string substitutions.

Upper Bounds on the Chromatic Index of Linear Hypergraphs
Thomas Murff, Xerxes D. Arsiwalla
This work studies upper bounds on the chromatic index of linear, loopless hypergraphs. The first bound is derived using a color-preserving group acting on a properly and minimally edge-colored hypergraph, where the group’s orbits create a finer partition of the coloring. This provides an upper bound on the chromatic index. The following results examine combinatorial properties of hypergraph coloring and outline a possible approach to the Berge–Füredi conjecture, linking the chromatic index to the maximum degree of the associated graph plus one. Three sufficient conditions are also identified for the conjecture to hold, involving the Helly property for hypergraphs.
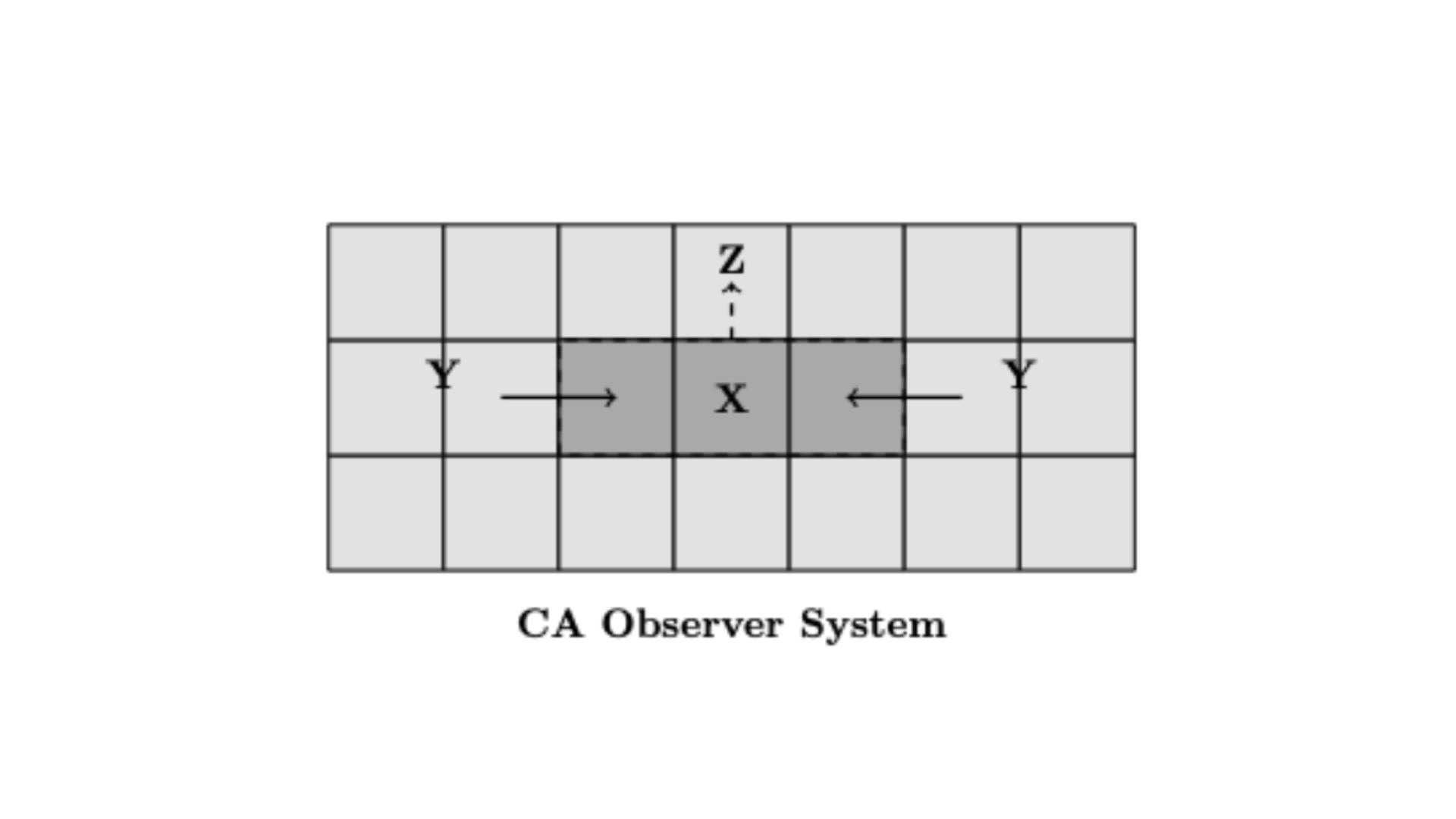
Towards a Generalized Theory of Observers
Hatem Elshatlawy, Xerxes Arsiwalla
A proposal of a formal framework for understanding and unifying the concept of observers across physics, computer science, philosophy, and related fields.

Non-Equilibrium Dynamics of Hard Spheres in the Fluid, Crystalline, and Glassy Regimes
Xerxes D. Arsiwalla, Matthew Kafker
An investigation of the response of a system of hard spheres to two classes of perturbations over a range of densities spanning the fluid, crystalline, and glassy regimes within a molecular dynamics framework.

Preons, Braid Topology, and Representations of Fundamental Particles
David Chester, Xerxes D. Arsiwalla, Louis H. Kauffman
Braided ribbon topology for representing Standard Model fermions and their interactions

Identifying and Manipulating Personality Traits in LLMs Through Activation Engineering
Rumi A. Allbert, James K. Wiles
An exploration into the latent space of Large Language Models to find and steer the personality of Generative Artificial Intelligence

Hypergraph rewriting and Causal structure of $\lambda$-calculus
Utkarsh Bajaj
Hypergraph rewriting is studied through categorical frameworks to establish foundational concepts of events and causality in graph rewriting systems. Novel concepts are introduced within double-pushout rewriting in adhesive categories. An algorithm is constructed to determine causal relations between events during λ-calculus evaluation, with extensions developed for arbitrary λ-expressions.

Quantum Potato Chips
Nikolay Murzin, Bruno Tenorio, Sebastian Rodriguez, John McNally, Mohammad Bahrami
This study maps qubit states under symmetric informationally-complete measurements to a tetrahedron in 3D space, identifying a "quantum potato chip" region where quantum states reduce to classical binary variables. States in this special region can be fully reconstructed using only two projective measurements, unlike states elsewhere in the quantum state space.

Why Does Biological Evolution Work? A Minimal Model for Biological Evolution and Other Adaptive Processes
Stephen Wolfram
Why does biological evolution work? And, for that matter, why does machine learning work? Both are examples of adaptive processes that surprise us with what they manage to achieve. So what’s the essence of what’s going on? I’m going to concentrate here on biological evolution, though much of what I’ll discuss is also relevant to machine learning—but I’ll plan to explore that in more detail elsewhere.
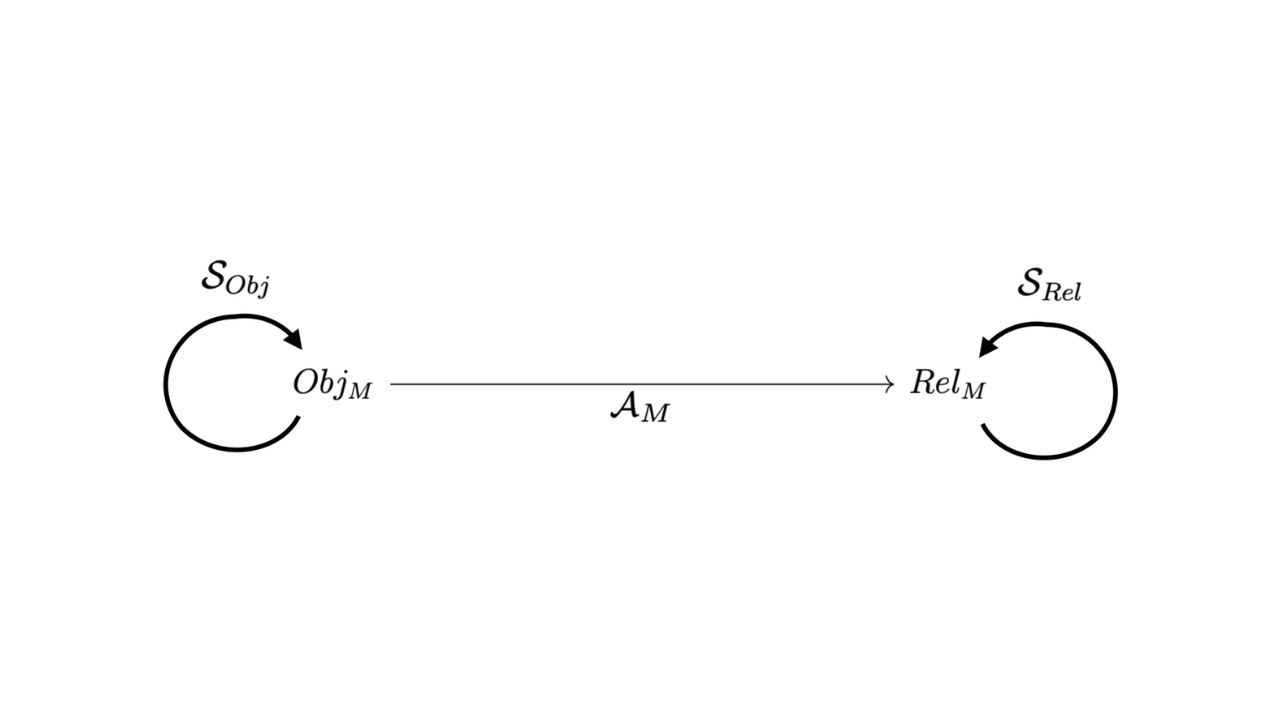
Qualia and the Formal Structure of Meaning
Xerxes D. Arsiwalla
This work explores the hypothesis that subjectively attributed meaning constitutes the phenomenal content of conscious experience. This form of subjective meaning manifests as an intrinsic and non-representational character of qualia.

An Invitation to Higher Arity Science
Carlos Zapata-Carratalá, Xerxes D. Arsiwalla
Exploration of a wide range of higher-order phenomena across multiple disciplines and the preliminary application of hypergraph and hypermatrix methods.

General Relativistic Hydrodynamics in Discrete Spacetime: Perfect Fluid Accretion onto Static and Spinning Black Holes
Jonathan Gorard
This study investigates the effect of spacetime discretization on accretion dynamics of a relativistic fluid onto a spinning black hole, specifically noting that accretion rates decrease with increased discretization scale and that drag force sensitivity and instabilities intensify at critical discretization values.

Computational General Relativity in the Wolfram Language using Gravitas II: ADM Formalism and Numerical Relativity
Jonathan Gorard
This paper introduces the Gravitas computational general relativity framework's numerical subsystem, emphasizing its ability to perform 3 + 1 spacetime decompositions via the ADM formalism, handle complex simulations of gravitational phenomena like binary black hole mergers, and leverage adaptive refinement algorithms based on hypergraph rewriting within the Wolfram Language.

On the operator origins of classical and quantum wave functions
Xerxes D. Arsiwalla, David Chester, Louis H. Kauffman
We investigate operator algebraic origins of the classical Koopman–von Neumann wave function $\psi_{KvN}$ as well as the quantum-mechanical one $\psi_{QM}$. In particular $\psi_{KvN}$, and $\psi_{QM}$ are both consequences of this pre-quantum formalism. What this suggests is that neither the Schrödinger equation nor the quantum wave function are fundamental structures.
Ruliology: Linking Computation, Observers and Physical Law
Dean Rickles, Hatem Elshatlawy, Xerxes D. Arsiwalla
Physical laws arise from the sampling of the Ruliad by observers (including us). This naturally leads to several conceptual issues, such as what kind of object is the Ruliad? What is the nature of the observers carrying out the sampling, and how do they relate to the Ruliad itself? What is the precise nature of the sampling? This paper provides a philosophical examination of these questions, and other related foundational issues, including the identification of a limitation that must face any attempt to describe or model reality in such a way that the modeller-observers are included.

Computational General Relativity in the Wolfram Language using Gravitas I: Symbolic and Analytic Computation
Jonathan Gorard
Gravitas introduces a robust computational framework for general relativity in the Wolfram Language, featuring seamless integration of symbolic and numerical tools to handle complex spacetime geometries and solve the Einstein field equations.
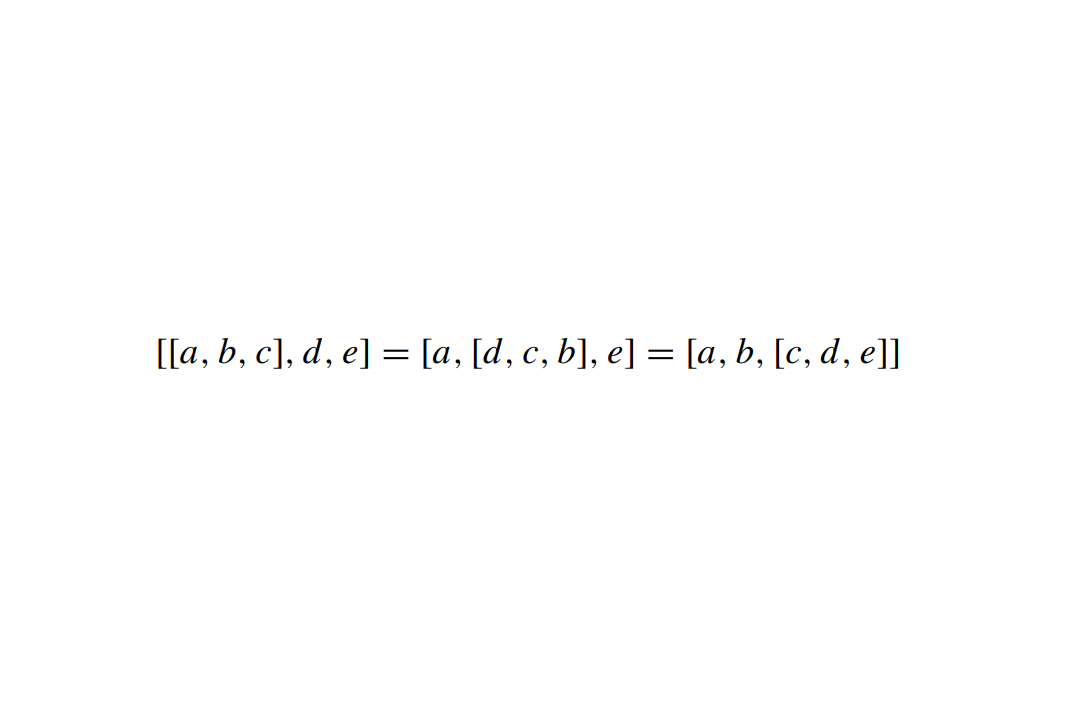
Biunit pairs in semiheaps and associated semigroups
Bernard Rybołowicz, Carlos Zapata-Carratalá
This research introduces biunit pairs in semiheaps, and establishes a direct correspondence between monoids with specific switches and semiheaps, leading to the novel concept of diheaps.

Hypermatrix Algebra and Irreducible Arity in Higher-Order Systems: Concepts and Perspectives
Carlos Zapata-Carratalá, Maximilian Schich, Taliesin Beynon, Xerxes D. Arsiwalla
Hypergraph and hypermatrix methods are applied to detect irreducible interactions in higher-order systems.

Non-Vacuum Solutions, Gravitational Collapse and Discrete Singularity Theorems in Wolfram Model Systems
Jonathan Gorard
This study extends the Raychaudhuri equation to discrete spacetimes, exploring conditions under which they might exhibit geodesic incompleteness, and applies numerical simulations to predict black hole formations.

Computational Foundations for the Second Law of Thermodynamics
Stephen Wolfram
Entropy increases. Mechanical work irreversibly turns into heat. The Second Law of thermodynamics is considered one of the great general principles of physical science. But 150 years after it was first introduced, there’s still something deeply mysterious about the Second Law. It almost seems like it’s going to be “provably true”. But one never quite gets there; it always seems to need something extra. Sometimes textbooks will gloss over everything; sometimes they’ll give some kind of “common-sense-but-outside-of-physics argument”. But the mystery of the Second Law has never gone away.
