Computational General Relativity in the Wolfram Language using Gravitas II: ADM Formalism and Numerical Relativity
Authors:
Jonathan Gorard
Abstract:
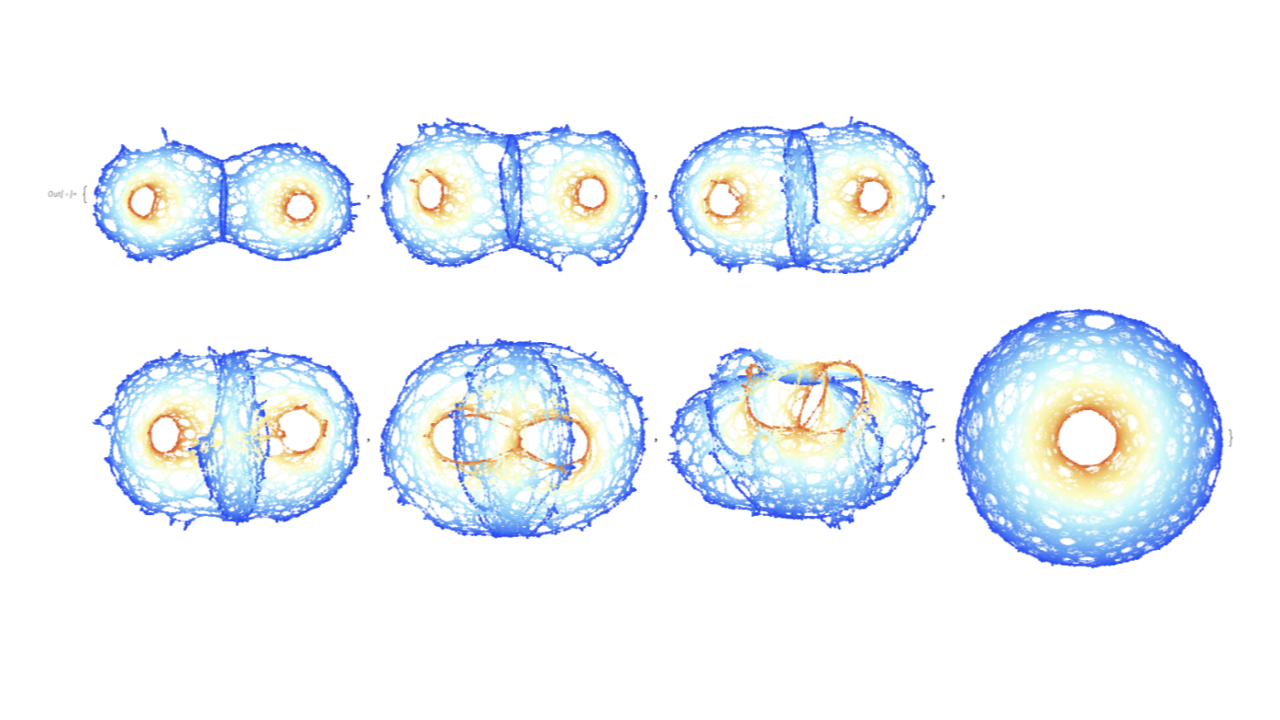
This is the second in a series of two articles introducing the Gravitas computational general relativity framework, in which we now focus upon the design and capabilities of Gravitas’s numerical subsystem, including its ability to perform general 3 + 1 decompositions of spacetime via the ADM formalism, its support for the definition and construction of arbitrary Cauchy surfaces as initial data, its support for the definition and enforcement of arbitrary gauge and coordinate conditions, its various algorithms for ensuring the satisfaction of the ADM Hamiltonian and momentum constraints, and its unique (totally-unstructured) adaptive refinement algorithms based on hypergraph rewriting via Wolfram model evolution. Particular attention will be paid to the seamless integration between Gravitas’s symbolic and numerical subsystems, its ability to configure, run, analyze and visualize complex numerical relativity simulations and their outputs within a single notebook environment, and its capabilities for handling generic curvilinear coordinate systems and spacetimes with general (and often highly nontrivial) topologies using its specialized and highly efficient hypergraph-based numerical algorithms. We also provide illustrations of Gravitas’s functionality for the visualization of hypergraph geometries and spacetime embedding diagrams in two and three dimensions, the ability for Gravitas’s symbolic and numerical subsystems to be used in concert for the extraction of gravitational wave signals and other crucial simulation data, and Gravitas’s in-built library of standard initial data, matter distributions and gauge conditions. We conclude by demonstrating how the numerical subsystem can be used to set up, run, visualize and analyze a standard yet nevertheless reasonably challenging numerical relativity test case: a binary black hole collision and merger within a vacuum spacetime (including the extraction of its outgoing gravitational wave profile).