What Are Lambdas?
It’s a story of pure, abstract computation. In fact, historically, one of the very first. But even though it’s something I for one have used in practice for nearly half a century, it’s not something that in all my years of exploring simple computational systems and ruliology I’ve ever specifically studied. And, yes, it involves some fiddly technical details. But it’ll turn out that lambdas—like so many systems I’ve explored—have a rich ruliology, made particularly significant by their connection to practical computing.
In Wolfram Language it’s the Function function. Back when Alonzo Church first discussed it in the 1930s he called it λ (lambda). The idea is to have something that serves as a “pure function”—which can be applied to an argument to give a value. For example, in the Wolfram Language one might have:
On its own it’s just a symbolic expression that evaluates to itself. But if we apply it to an argument then it substitutes that argument into its body, and then evaluates that body:
In the Wolfram Language we can also write this as:
Or, with λ = Function, we can write
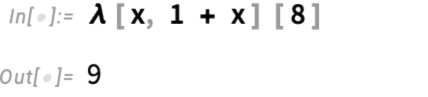
which is close to Church’s original notation (λx .(1 + x)) 8.
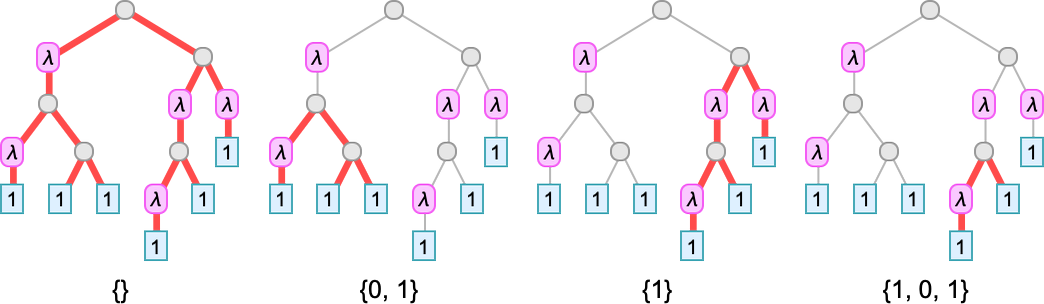
But what if we want to “go even purer”, and effectively just “use λ for everything”—without any pre-defined functions like Plus (+)? To set up lambdas at all, we have to have a notion of function application (as in f[x] meaning “apply f to x”). So, for example, here’s a lambda (“pure function”) that just has a structure defined by function application:
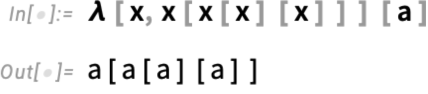
Can we do familiar operations with this kind of setup? Let’s imagine we have a symbol z that represents 0, and another symbol s that represents the operation of computing a successor. Then here’s a representation of the integers 0 through 5:
But let’s look for example at s[s[s[s[z]]]]. We can “factor out” the s and z in this expression and write the “purely structural” part just in terms of lambdas:
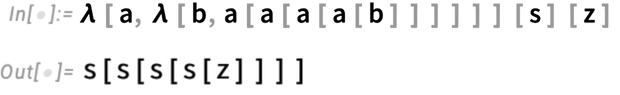
But in a sense we don’t need the s and z here; we can perfectly well set up a representation for integers just in terms of lambdas, say as (often known as “Church numerals”):
It’s all very pure—and abstract. And, at least at first, it seems very clean. But pretty soon one runs into a serious problem. If we were to write
what would it mean? In x[x] are the x’s associated with the x in the inner λ or the outer one? Typing such an expression into the Wolfram Language, x’s turn red to indicate that there’s a problem:
And at this level the only way to resolve the problem is to use different names for the two x’s—for example:
But ultimately the particular names one uses don’t matter. For example, swapping x and y
represents exactly the same function as before.
How can one deal with this? One approach—that was actually invented more than a decade before lambdas, and that I in fact wrote a whole book about a few years ago—is to use so-called “combinators”: constructs that in effect abstractly define how to rearrange symbolic expressions, without having to name anything, or, for that matter, introduce variables at all. So, for example, λ[x, λ[y, y[x]]] can be written
as one can confirm using:
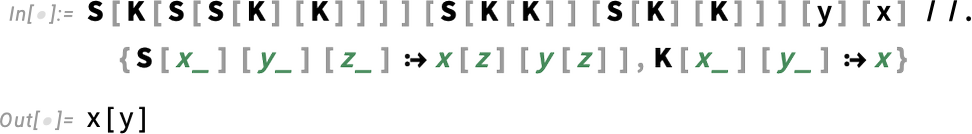
At some level this is very elegant. But, yes, it’s extremely difficult to read. So is there a way to preserve at least some of the comparative readability of lambdas without having to explicitly introduce variables with names, etc.? It turns out there is. And it starts from the observation that a named variable (say x) is basically just a way of referring back to the particular lambda (say λ[x, …]) that introduced that variable. And the idea is that rather than making that reference using a named variable, we make it instead by saying “structurally” where the lambda is relative to whatever is referring to it.
So, for example, given
we can write this in the “de Bruijn index” (pronounced “de broin”) form
where the 1 says that the variable in that position is associated with the λ that’s “one λ back” in the expression, while that 2 says that the variable in that position is “two λ’s back” in the expression:
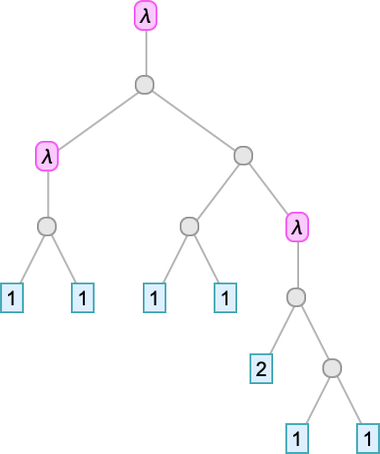
So, for example, our version of the integers as lambdas can now be written as:
OK, so lambdas can represent things (like integers). But can one “compute with lambdas”? Or, put another way, what can pure lambdas do?
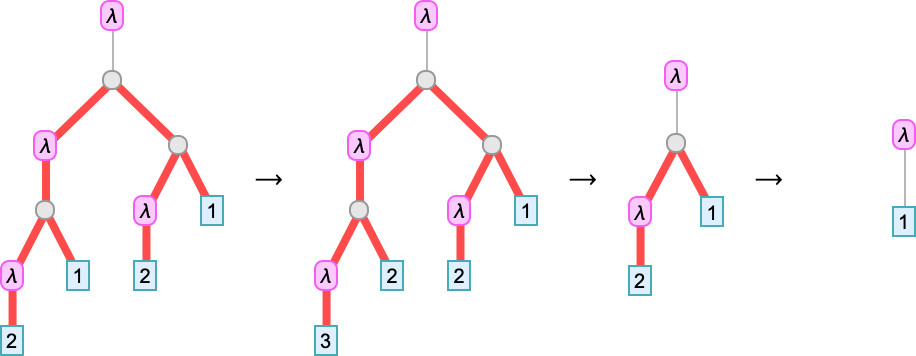
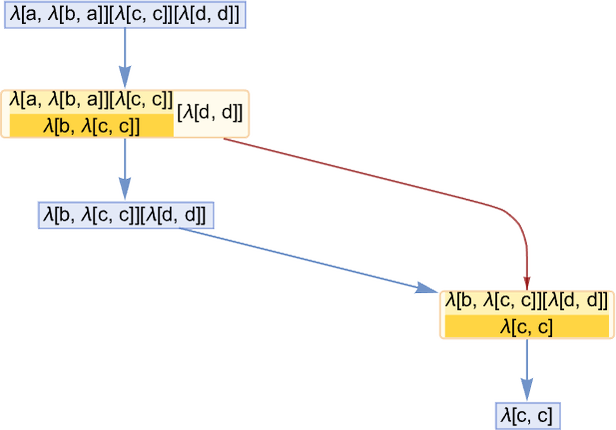
Fundamentally, there’s just one operation—usually called beta reduction—that takes whatever argument a lambda is given, and explicitly “injects it” into the body of the lambda, in effect implementing the “structural” part of applying a function to its argument. A very simple example of beta reduction is
which is equivalent to the standard Wolfram Language evaluation:
In terms of de Bruijn indices this becomes
which can again be “evaluated” (using beta reduction) to be:
This seems like a very simple operation. But, as we’ll see, when applied repeatedly, it can lead to all sorts of complex behavior and interesting structure. And the key to this turns out to be the possibility of lambdas appearing as arguments of other lambdas, and through beta reduction being injected into their bodies.
But as soon as one injects one lambda into another, there are tricky issues that arise. If one writes everything explicitly with variables, there’s usually variable renaming that has to be done, with, for example
evaluating to:
In terms of de Bruijn indices there’s instead renumbering to be done, so that
evaluates to:
It’s easy to describe informally what beta reduction is doing. In Wolfram Language terms it’s basically just the transformation:
In other words, given λ[x, body][y], beta reduction is replacing every instance of x in body with y, and returning the result. But it’s not quite as simple as that. For example, if y contains a lambda—as in the example above—then we may have to do a certain amount of renaming of variables (usually called “alpha conversion”). And, yes, there can potentially be a cascade of renamings. And you might have to come up with an arbitrary number of distinct new names to use in these renamings.
And once you’ve done the substitution (“beta reduction”) of λ[x, body][y] this can “expose” another lambda in which you have to do more substitution, and so on. This might sound like a detail. But actually it’s quite fundamental—and it’s what lets lambdas represent computations that “keep running”, and that give rise to the rich ruliology we’ll discuss here.
Is it somehow easier to do beta reduction with de Bruijn indices? No, not really. Yes, you don’t have to invent names for variables. But instead you have to do rather fiddly recursive realignment of indices whenever you’re in effect inserting or deleting lambdas.
There’s another issue as well. As we’ll explore in detail later, there are often multiple beta reductions that can be done on a given lambda. And if we trace all the possibilities we get a whole multiway graph of possible “paths of lambda evaluation”. But a fundamental fact about lambdas (known as confluence or the Church–Rosser property, and related to causal invariance) is that if a sequence of beta reductions for a given lambda eventually reaches a fixed point (which, as we’ll see, it doesn’t always), that fixed point will be unique: in other words, evaluating the lambda will always give a definite result (or “normal form”).
So what should one call the things one does when one’s working with lambdas? In Wolfram Language we talk of the process of, say, turning Function[x, x[x]][a] (or λ[x, x[x]][a]) into a[a] as “evaluation”. But sometimes it’s instead called, for example, reduction or conversion or substitution or rewriting. In Wolfram Language we might also call λ[…] a “λ expression”, but it’s also sometimes called a λ term. What about what’s inside it? In λ[x, body] the x is usually called a “bound variable”. (If there’s a variable—say y—that appears in body and that hasn’t been “bound” (or “scoped”) by a λ, it’s called a “free variable”. The λ expressions that we’ll be discussing here normally have no free variables; such λ expressions are often called “closed λ terms”. )
Putting a lambda around something—as in λ[x, thing]—is usually called “λ abstraction”, or just “abstraction”, and the λ itself is sometimes called the “abstractor”. Within the “body” of a lambda, applying x to y to form x[y] is—not surprisingly—usually called an “application” (and, as we’ll discuss later, it can be represented as x@y or x•y). What about operations on lambdas? Historically three are identified: α reduction (or α conversion), β reduction (or β conversion) and η reduction (or η conversion). β reduction—which we discussed above—is really the core “evaluation-style” operation (e.g. replacing λ[x, f[x]][y] with f[y]). α and η reduction are, in a sense, “symbolic housekeeping operations”; α reduction is the renaming of variables, while η reduction is the reduction of λ[x, f[x]] to f alone. (In principle one could also imagine other reductions—say transformations directly defined for λ[_][_][_]—though these aren’t traditional for lambdas.)
The actual part of a lambda on which a reduction is done is often called a “redex”; the rest of the lambda is then the “context”—or “an expression with a hole”. In what we’ll be doing here, we’ll mostly be concerned with the—fundamentally computational—process of progressively evaluating/reducing/converting/… lambdas. But a lot of the formal work done in the past on lambdas has concentrated on the somewhat different problem of the “calculus of λ conversion”—or just “λ calculus”—which concentrates particularly on identifying equivalences between lambdas, or, in other words, determining when one λ expression can be converted into another, or has the same normal form as another.
By the way, it’s worth saying that—as I mentioned above—there’s a close relationship between lambdas and the combinators about which I wrote extensively a few years ago. And indeed many of the phenomena that I discussed for combinators will show up, with various modifications, in what I write here about lambdas. In general, combinators tend to be a bit easier to work with than lambdas at a formal and computational level. But lambdas have the distinct advantage that at least at the level of individual beta reductions it’s much easier to interpret what they do. The S combinator works in a braintwisting kind of way. But a beta reduction is effectively just “applying a function to an argument”. Of course, when one ends up doing lots of beta reductions, the results can be very complicated—which is what we’ll be talking about here.
Basic Computation with Lambdas
How can one do familiar computations just using lambdas? First, we need a way to represent things purely in terms of lambdas. So, for example, as we discussed above, we can represent integers using successive nesting. But now we can also define an explicit successor function purely in terms of lambdas. There are many possible ways to do this; one example is
where this is equivalent to:
Defining zero as
or
we can now form a representation of the number 3:
But “evaluating” this by applying beta reduction this turns out to reduce to
which was exactly the representation of 3 that we had above.
Along the same lines, we can define
(where these functions take arguments in “curried” form, say, times[3][2], etc.).
So then for example 3×2 becomes
which evaluates (after 37 steps of beta reduction) to:
Applying this to “unevaluated” s and z we get
which under beta reduction gives
which we can recognize as our representation for the number 6.
And, yes, we can go further. For example, here’s a representation (no doubt not the minimal one) for the factorial function in terms of pure lambdas:
And with this definition
i.e. 4!, indeed eventually evaluates to 24:
Later on we’ll discuss the process of doing an evaluation like this and we’ll see that, yes, it’s complicated. In the default way we’ll carry out such evaluations, this particular one takes 5067 steps (for successive factorials, the number of steps required is 41, 173, 864, 5067, 34470, …).
Ways to Write Lambdas
From what we’ve seen so far, one obvious observation about lambdas is that—except in trivial cases—they’re pretty hard to read. But do they need to be? There are lots of ways to write—and render—them. But what we’ll find is that while different ones have different features and advantages (of which we’ll later make use), none of them really “crack the code” of making lambdas universally easy for us to read.
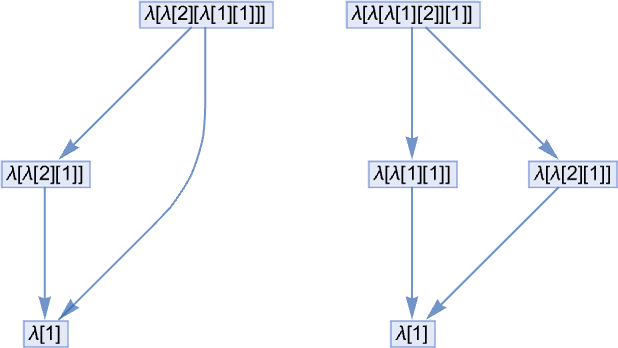
Let’s consider the following lambda, written out in our standard textual way:
This indicates how the variables that appear are related:
And, yes, since each λ “scopes” its bound variable, we could as well “reuse” y in place of z:
One obvious thing that makes an expression like this hard to read is all the brackets it contains. So how can we get rid of these? Well, in the Wolfram Language we can always write f@x in place of f[x]:
And, yes, because the @ operator in the Wolfram Language associates to the right, we can write f@g@x to represent f[g[x]]. So, OK, using @ lets us get rid of quite a few brackets. But instead it introduces parentheses. So what can we do about these? One thing we might try is to use the application operator • (Application) instead of @, where • is defined to associate to the left, so that f•g•x is f[g][x] instead of f[g[x]]. So in terms of • our lambda becomes:
The parentheses moved around, but they didn’t go away.
We can make these expressions look a bit simpler by using spaces instead of explicit @ or •. But to know what the expressions mean we have to decide whether spaces mean @ or •. In the Wolfram Language, @ tends to be much more useful than • (because, for example, f@g@x conveniently represents applying one function, then another). But in the early history of mathematical logic, spaces were effectively used to represent •. Oh, and λ[x, body] was written as λx . body, giving the following for our example lambda:
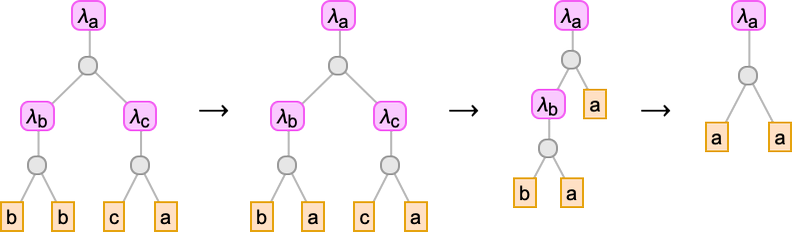
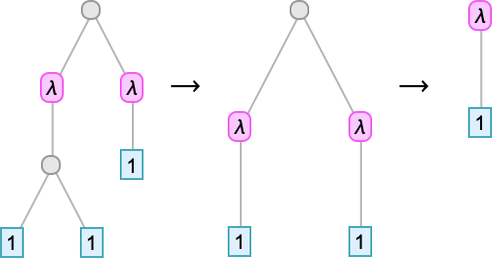
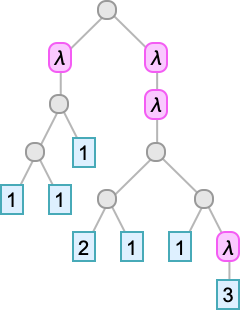
We’ve been trying to write lambdas out in linear form. But in some sense, they’re always really trees—just like expressions in the Wolfram Language are trees. So here for example is
shown as a tree:
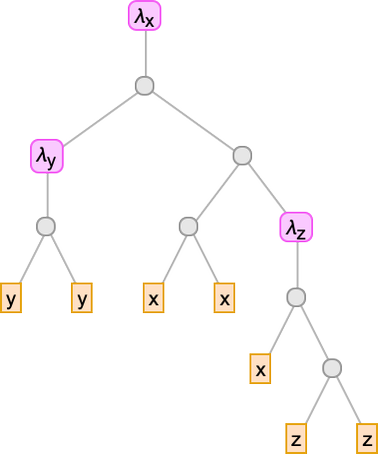
The leaves of the tree are variables. The intermediate nodes are either λ[…, …]’s (“abstractions”) or …[…]’s (“applications”). Everything about lambdas can be done in this tree representation. So, for example, beta reduction can be thought of as a replacement operation on a piece of the tree representing a lambda:
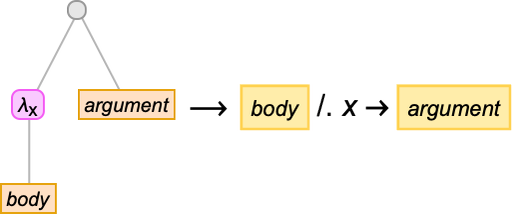
But, OK, as we discussed above, it never matters what specific names have been given to the variables. All that matters is what lambdas they’re associated with. And we can indicate this by overlaying appropriate connections on the tree:
But what if we just route these connections along the branches in the tree?
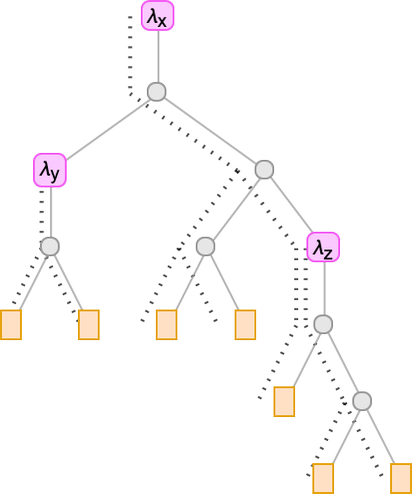
To find out which λ a given variable goes with, we just have to count how many λ’s we encounter walking up the tree from the leaf representing that variable before we reach “its λ”. So this means we can represent the lambda just by filling in a number at each leaf of the tree:
And these numbers are precisely the de Bruijn indices we discussed earlier. So now we’ve seen that we can replace our “named variables” lambda tree with a de Bruijn index lambda tree.
Writing this particular tree out as an expression we get:
The λ’s now don’t have any explicit variables specified. But, yes, the expression is “hooked up” the same way it was when we were explicitly using variables:
Once again we can get rid of our “application brackets” by using the • (Application) operator:
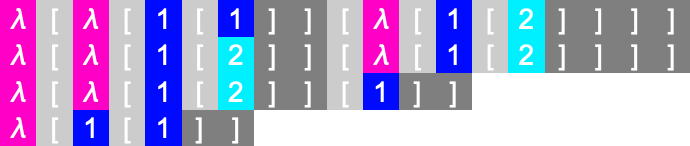
And actually we don’t really need either the •’s or even the λ’s here: everything can be deduced just from the sequence of brackets. So in the end we can write our lambda out as
where there’s an “implicit λ” before every “[” character, and an implicit • between every pair of digits. (Yes, we’re only dealing with the case where all de Bruijn indices are below 10.)
So now we have a minimal way to write out a lambda as a string of characters. It’s compact, but hard to decode. So how can we do better?
At the very simplest level, we could, for example, color code every character (here with explicit λ’s and brackets included):
And indeed we’ll find this representation useful later.
But any “pure string” makes the nesting structure of the lambda visible only rather implicitly, in the sequence of brackets. So how can we make this more explicit? Well, we could explicitly frame each nested λ:
Or we could just indicate the “depth” of each element—either “typographically”
or graphically (where the depth is TreeDepth):
We can think of this as a kind of one-dimensionally-unrolled version of a tree representation of lambdas. Another approach is in effect to draw the tree on a 2D grid—to form what we can call a Tromp diagram:
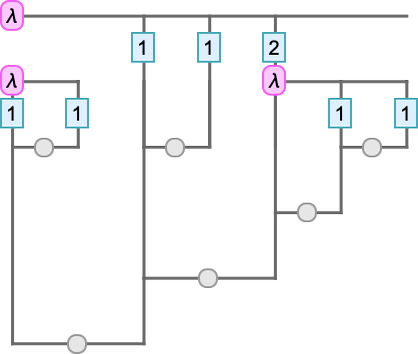
To see what’s going on here, we can superimpose our standard tree on the Tromp diagram:
Each vertical line represents an instance of a variable. The top of the line indicates the λ associated with that variable—with the λ being represented by a horizontal line. When one instance of a variable is applied to another, as in u[v], there is a horizontal line spanning from the “u” vertical line to the “v” one.
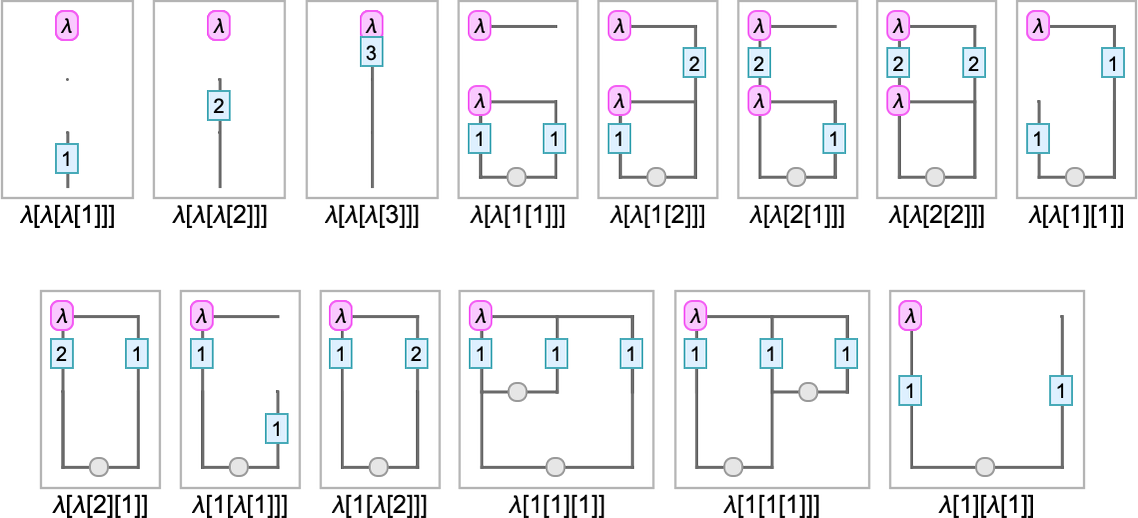
And with this setup, here are Tromp diagrams for some small lambdas:
Another graphical approach is to use “string diagrams” that directly show how the elements of lambdas are “wired up”. Consider for example the simple lambda:
This can be represented as the string diagram:
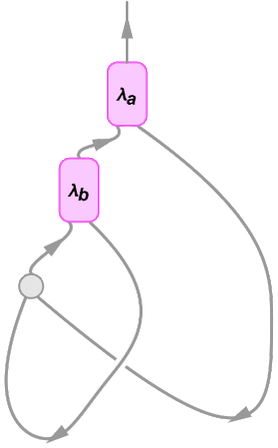
The connectivity here is the same as in:
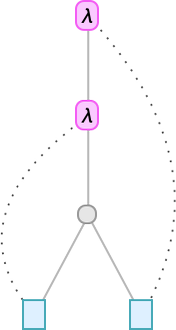
In the string diagram, however, the explicit variables have been “squashed out”, but are indicated implicitly by which λ’s the lines correct back to. At each λ node there is one outgoing edge that represents the argument of the λ, and one incoming edge that connects to its body. Just as when we represent the lambda with a tree, the “content” of the lambda “hangs off” the top of the diagram.
Here are examples of string diagrams for a few small lambdas:
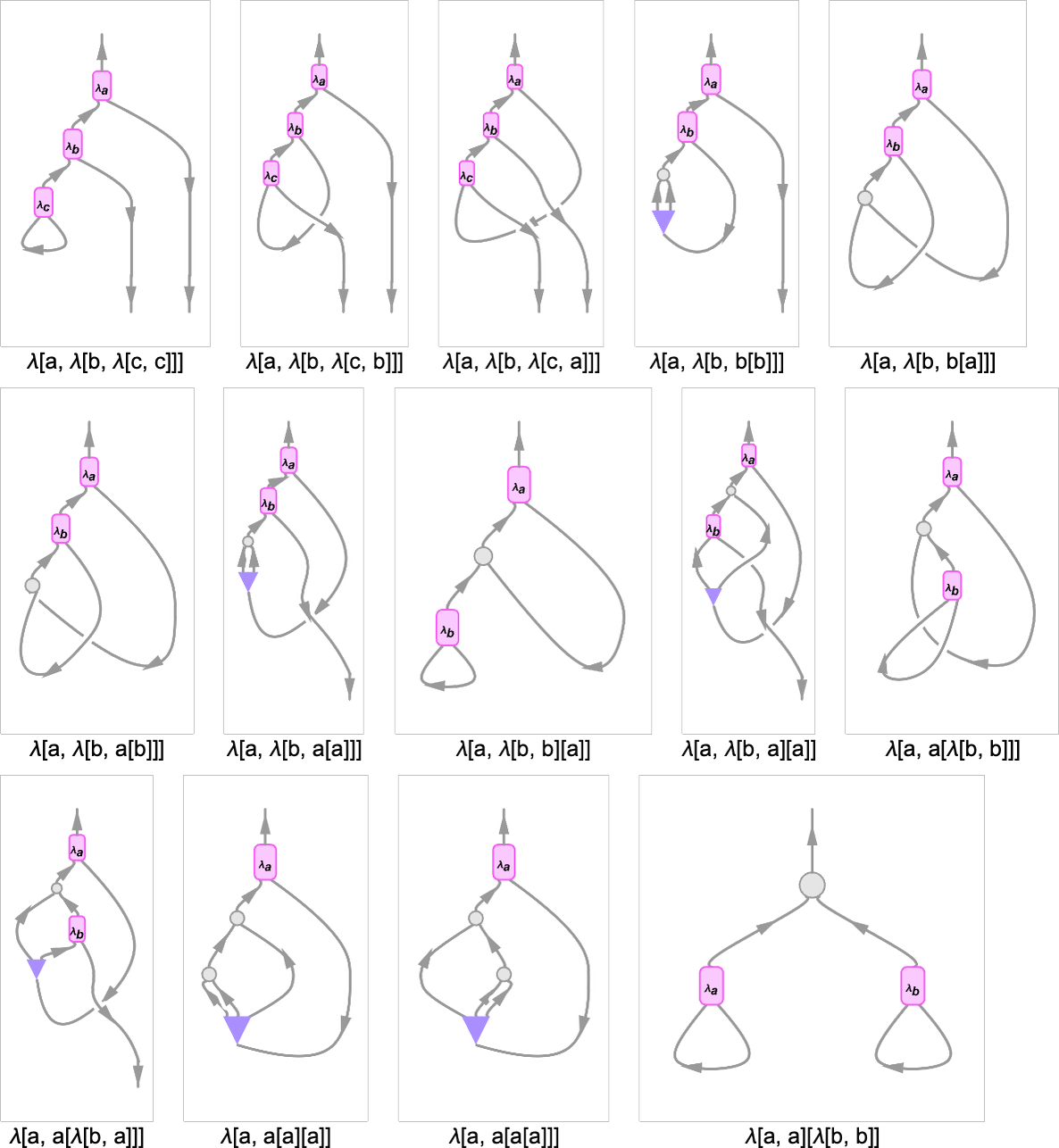
In these diagrams, the edges that “exit the diagram” at the bottom correspond to variables that are
unused in the the lambda. The “cups” that appear in the diagrams correspond to “variables that are
immediately used”, as in λ[x, x]. What about the 
in, for example,
λ[a,λ[b,b[b]]]? It represents the copying of a variable, which is needed here because
b is used twice in the lambda.
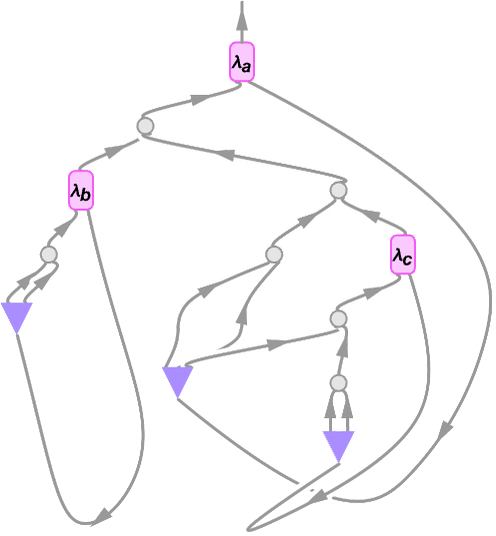
Returning to our previous example (now written with explicit variables)
here is the (somewhat complicated) string diagram corresponding to this lambda:
One can think of a string diagram like this as somehow defining the “flow of symbolic content” through “pipes” associated with variables. But is there some purer way to represent such flows, without ever having to introduce variables? Well, yes there is, and it’s to use combinators. And indeed there’s an immediate correspondence between combinator expressions and lambdas. So, for example
can be represented in terms of combinators by:
As is typical of combinators, this is in a sense very pure and uniform, but it’s also very difficult to
interpret. And, yes, as we’ll discuss later, small lambda expressions can correspond to large combinator
expressions. And the same is true the other way around, so that, for example, 
becomes as a lambda expression
or in compact form:
But, OK, this compact form is in some sense a fairly efficient representation. But it has some hacky features. Like, for example, if there are de Bruijn indices whose values are more than one digit long, they’ll need to be separated by some kind of “punctuation”.
But what if we insist on representing a lambda expression purely as a sequence of 0’s and 1’s? Well, one thing we can do is to take our compact form above, represent its “punctuation characters” by fixed strings, and then effectively represent its de Bruijn indices by numbers in unary—giving for our example above:
This procedure can be thought of as providing a way to represent any lambda by an integer (though it’s certainly not true that it associates every integer with a lambda).
Enumerating Lambdas
To begin our ruliological investigation of lambdas and what they do, we need to discuss what possible forms of lambdas there are—or, in other words, how to enumerate lambda expressions. An obvious strategy is to look at all lambda expressions that have progressively greater sizes. But what is the appropriate measure of “size” for a lambda expression?
Mostly here we’ll use Wolfram Language LeafCount. So, for example
will be considered to have “size” 10 because in the most direct Wolfram Language tree rendering
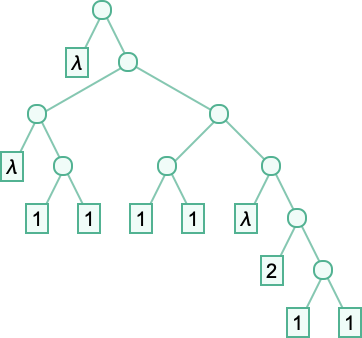
there are 10 “leaves”. We’ll usually render lambdas instead in forms like
in which case the size is the number of “de Bruijn index leaves” or “variable leaves” plus the number of λ’s.
(Note that we could consider alternative measures of size in which, for example, we assign different weights to abstractions (λ’s) and to applications, or to de Bruijn index “leaves” with different values.)
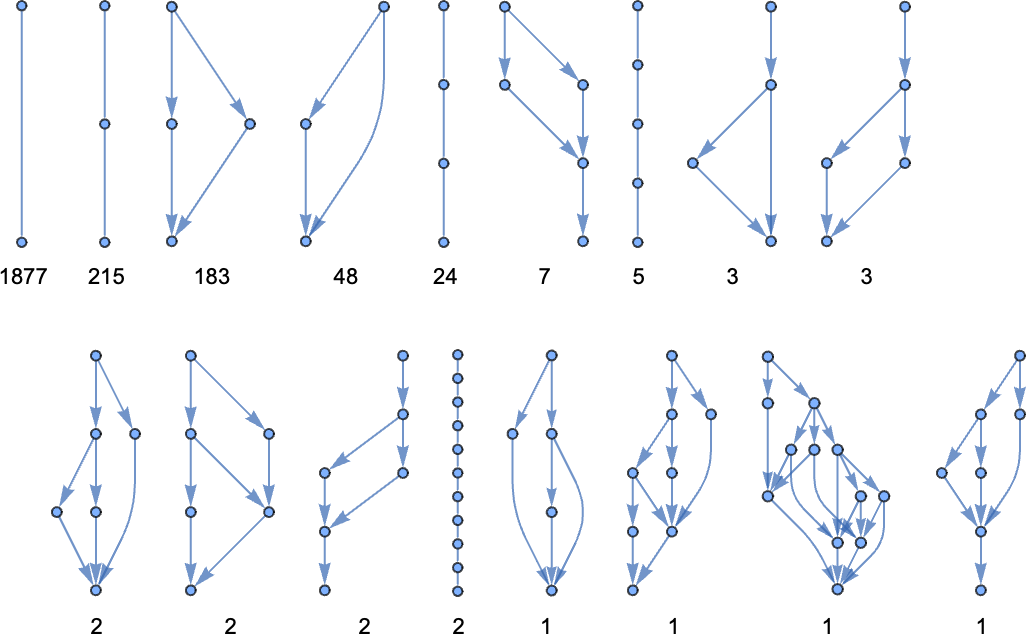
Using LeafCount as our measure, there are then, for example, 14 lambdas of size 4:
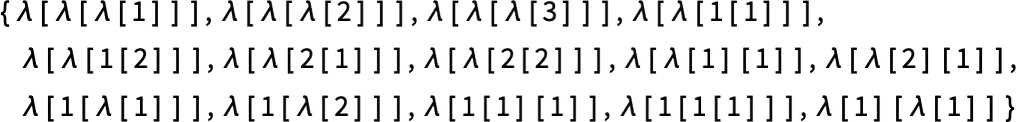
As trees these become
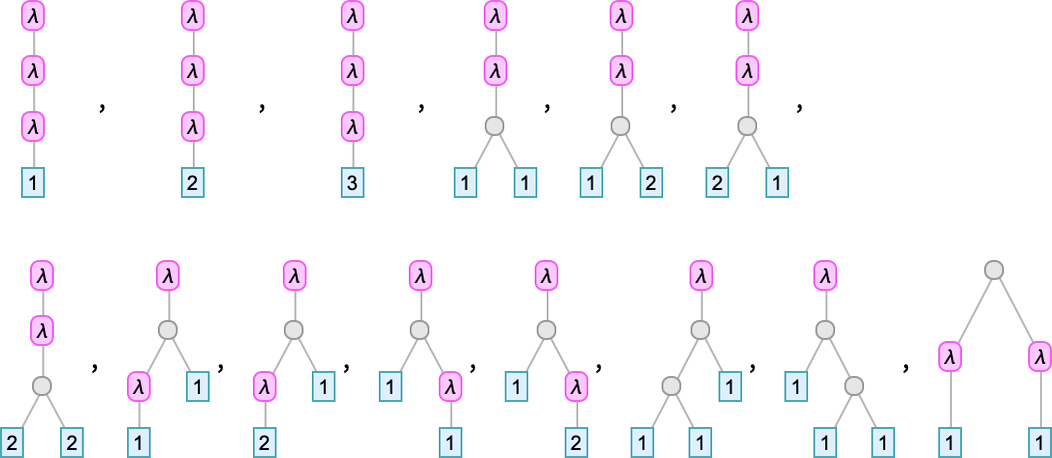
while as Tromp diagrams they are:
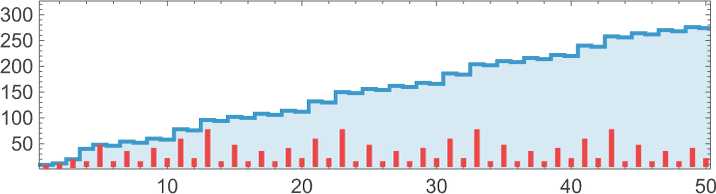
The number of lambdas grows rapidly with size:
These numbers are actually given by c[n,0] computed from the simple recurrence:
For large n, this grows roughly like n!, though apparently slightly slower.
At size n, the maximum depth of the expression tree is 
; the mean is roughly 
and the limiting distribution is:
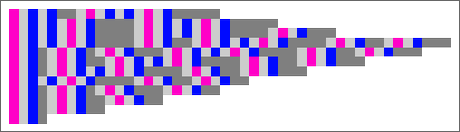
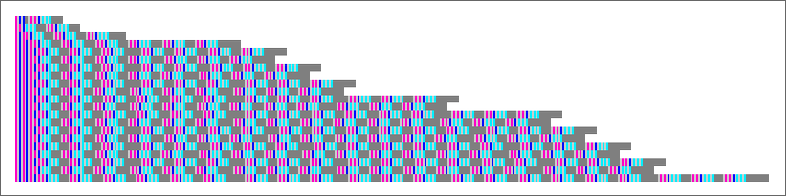
We can also display the actual forms of the lambdas, with a notable feature being the comparative diversity of forms seen:
The Evaluation of Lambdas
What does it mean to “evaluate” a lambda? The most obvious interpretation is to do a sequence of beta reductions until one reaches a “fixed point” where no further beta reduction can be done.
So, for example, one might have:
If one uses de Bruijn indices, beta reduction becomes a transformation for λ[_][_], and our example becomes:
In compact notation this is
while in terms of trees it is:
By rendering the characters in the de Bruijn index form as color squares, we can also represent this evolution in the “spacetime” form:
But what about other lambdas? None of the lambdas of size 3
contain the pattern λ[_][_], and so none of them allow beta reduction. At size 4 the same is true of most of the 14 possible lambdas, but there is one exception, which allows a single step of beta reduction:
At size 5, 35% of the lambdas aren’t inert, but they still have short “lifetimes”
with the longest “evaluation chain” being:
At size 6, 44% of lambdas allow beta reductions, and aren’t immediately inert:
A couple of lambdas have length-4 evaluation chains:
And now there’s something new—a period-1 “looping lambda” (or “quine”) that just keeps on transforming into itself under beta reduction, and so never reaches a fixed point where no beta reduction can be applied:
At size 7, just over half of the lambdas aren’t inert:
There are a couple of “self-repeating” lambdas:
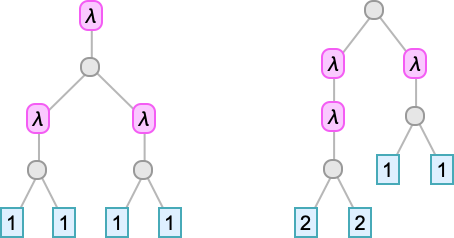
The first is a simple extension of the self-repeating lambda at size 6; the second is something at least slightly different.
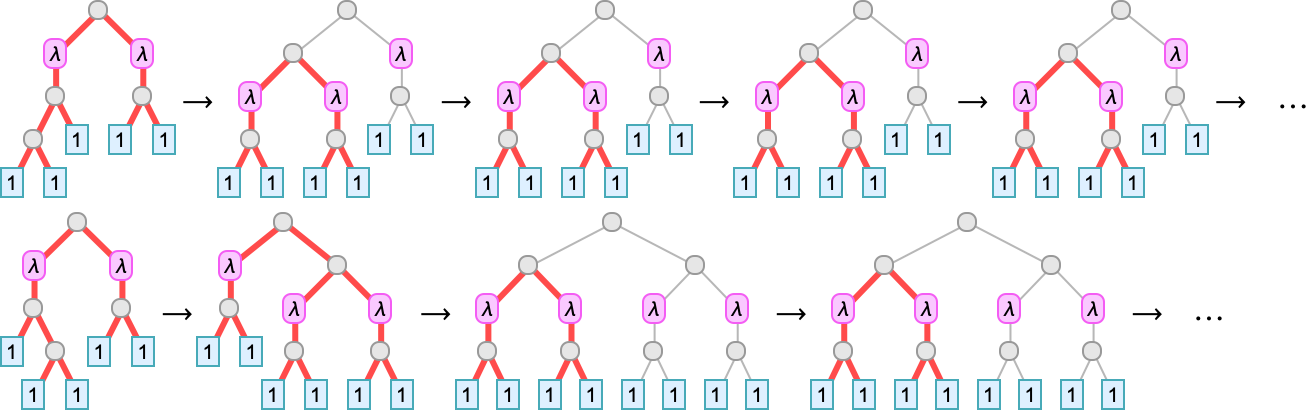
At size 7 there are also a couple of cases where there’s a small “transient” before a final repeating state is reached (here shown in compact form):
Here’s what happens with the lambda trees in this case—where now we’ve indicated in red the part of each tree involved in each beta reduction:
And there’s also something new: three cases where beta reduction leads to lambdas that grow forever. The simplest case is
which grows in size by 1 at each step:
Then there’s
which, after a single-step transient, grows in size by 4 at each step:
And finally there’s
which grows in a slightly more complicated way
alternating between growing by 4 and by 12 on successive steps (so at step t > 1 it is of size 8t – 4 Mod[t + 1, 2]):
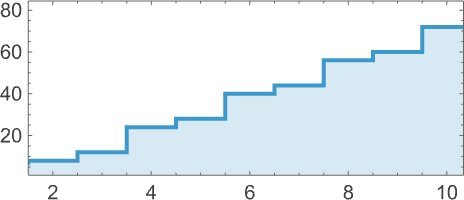
If we look at what’s happening here “underneath”, we see that beta reduction is just repeatedly getting applied to the first λ at each step:
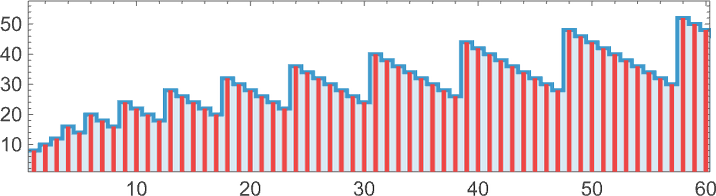
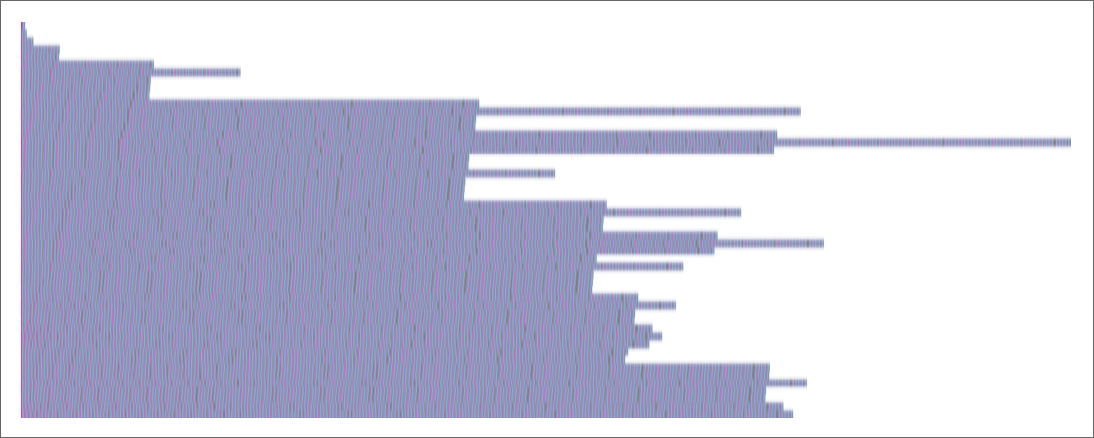
And we can conveniently indicate this when we plot the successive sizes of lambdas:
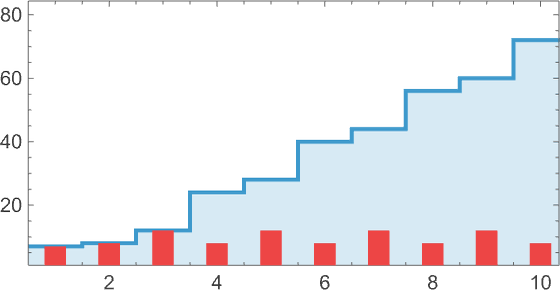
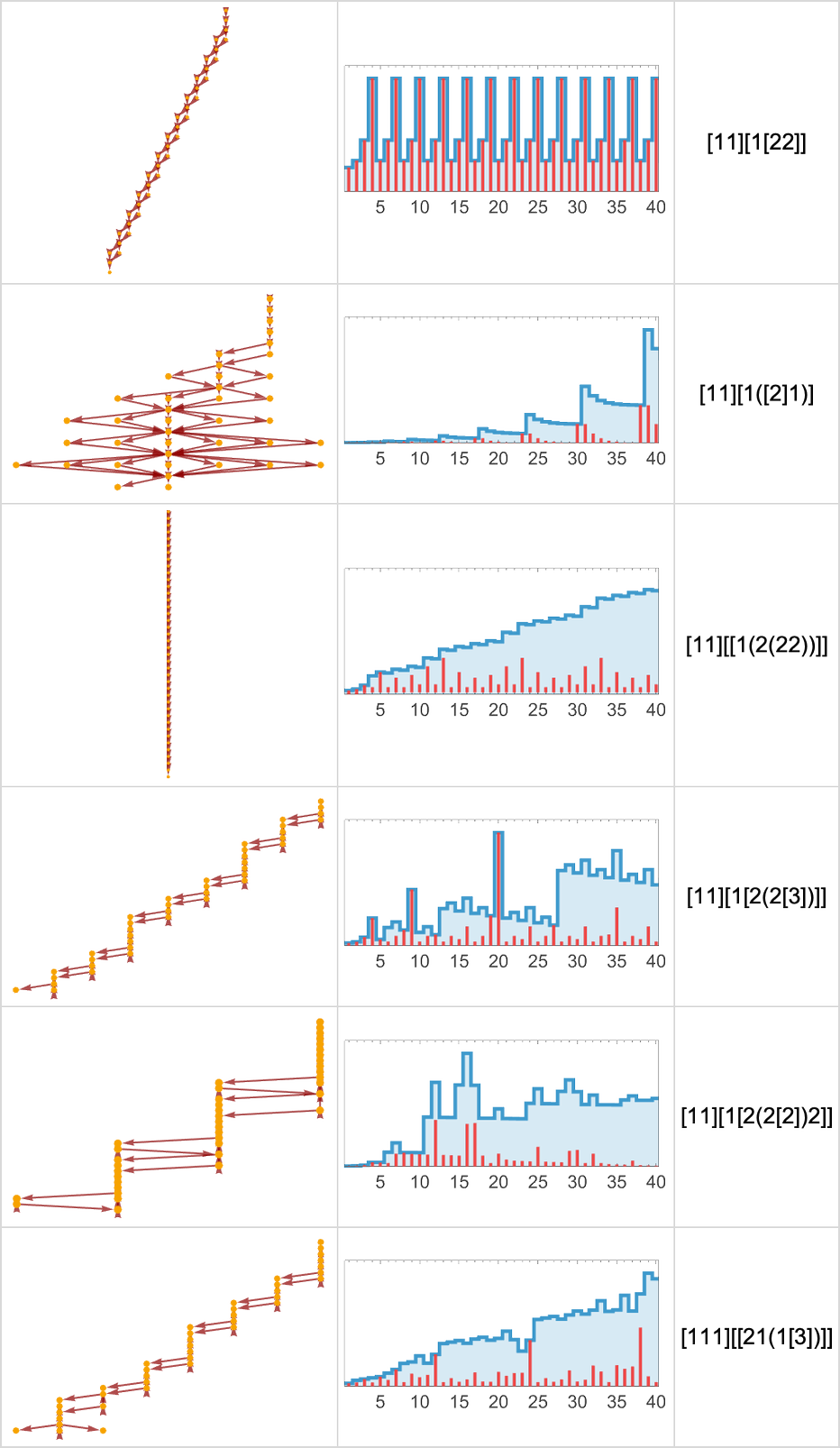
At size 8, things begin to get more interesting. Of the 43,977 possible lambdas, 55% aren’t inert:
The longest evaluation chain that terminates occurs for
and is of length 12:
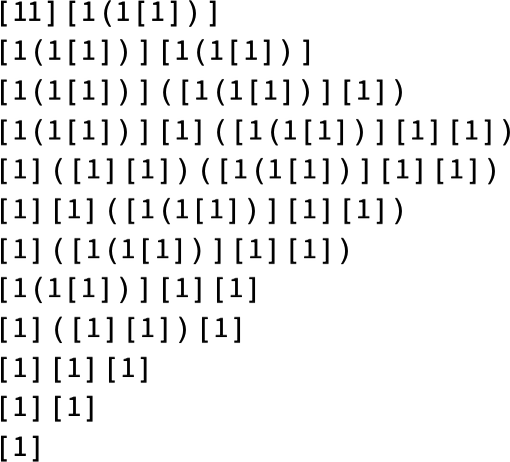
Among all 43,977 size-8 lambdas, there are only 164 distinct patterns of growth:
The 81 lambdas that don’t terminate have various patterns of growth:
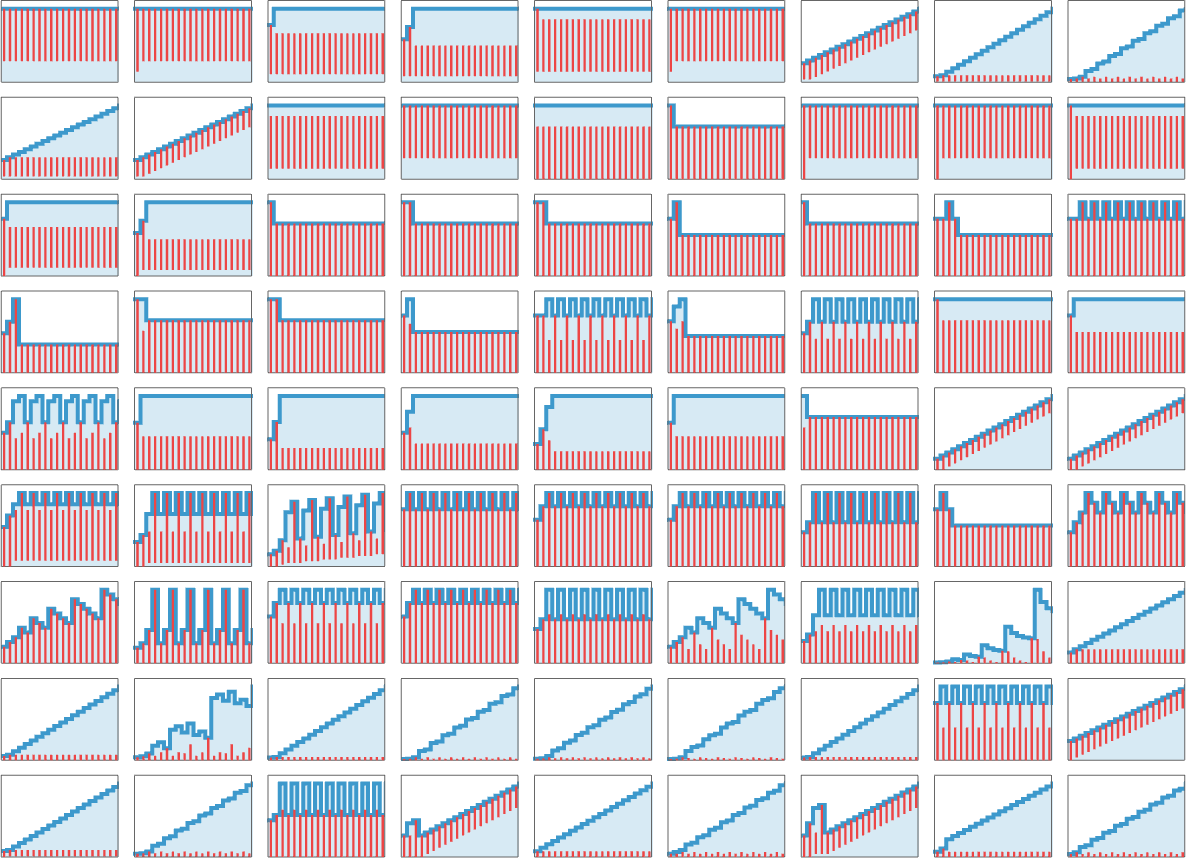
Some, such as
alternate every other step:
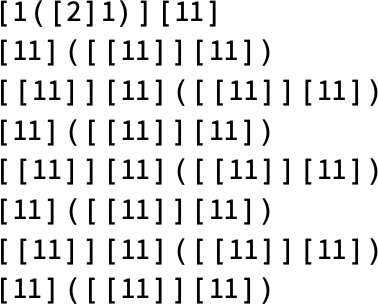
Others, such as
have period 3:
Sometimes, as in
there’s a mixture of growth and periodicity:
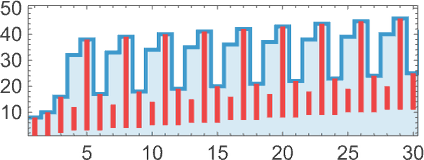
There’s simple nested behavior, as in
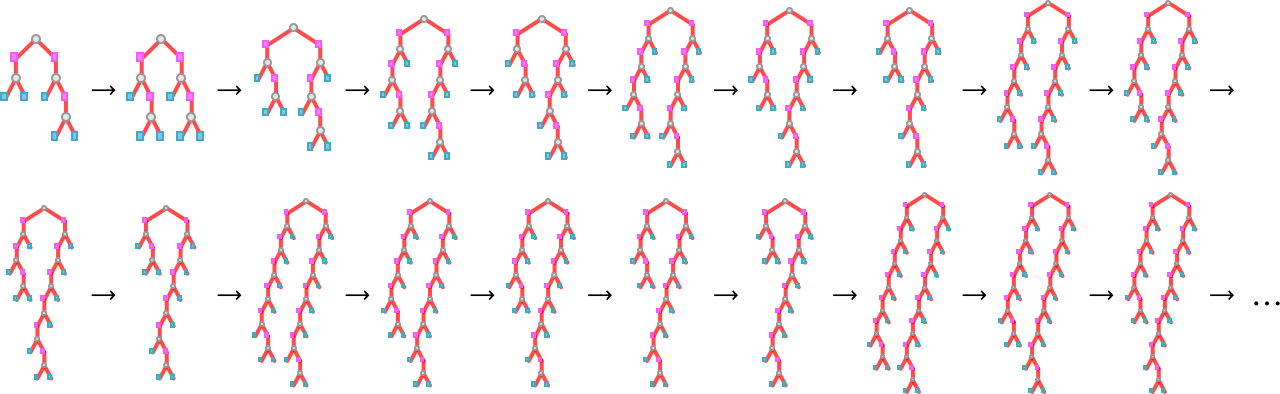
where the envelope grows like 
.
There’s more elaborate nested behavior in
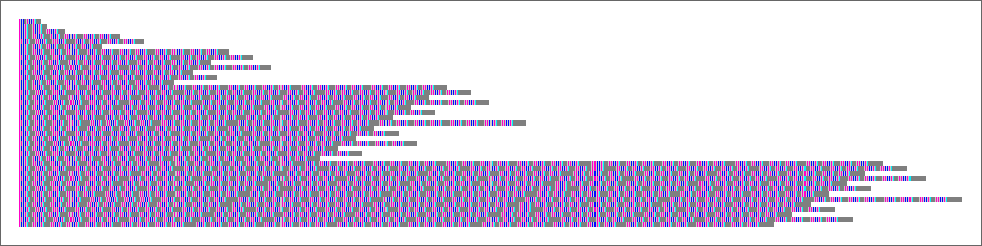
where now the envelope grows linearly with t.
Finally, there’s
which instead shows highly regular 
growth:
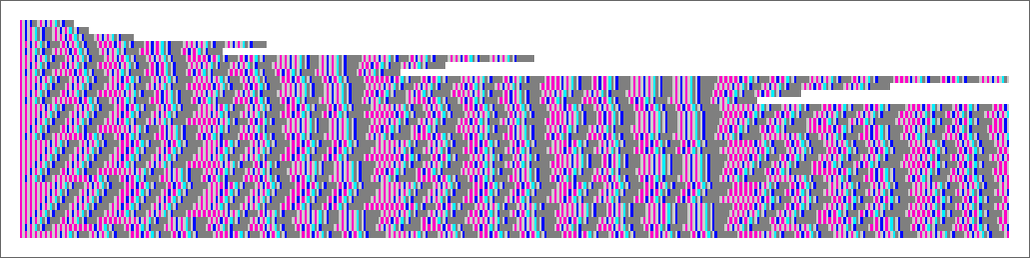
And the conclusion is that for lambdas up to size 8, nothing more complicated than nested behavior occurs. And in fact in all these cases it’s possible to derive exact formulas for the size at step t.
To see roughly how these formulas work, we can start with the sequence:
This sequence turns out to be given by the nestedly recursive recurrence
and the tth term here is just:
For the first nested sequence above, the corresponding result is (for t > 1):
For the second one it is (for t > 3):
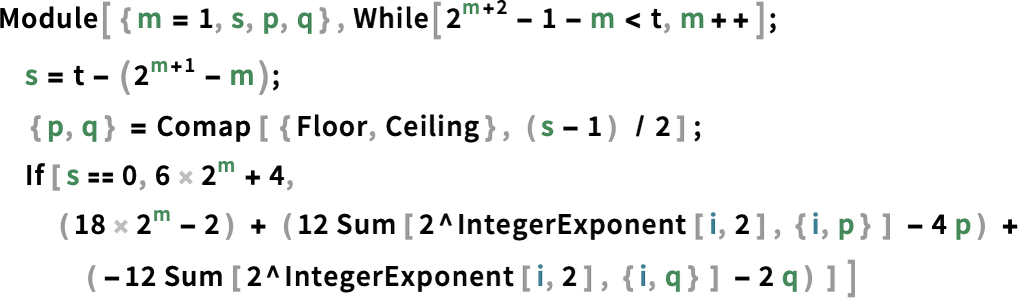
And for third one it is (for t > 1) :
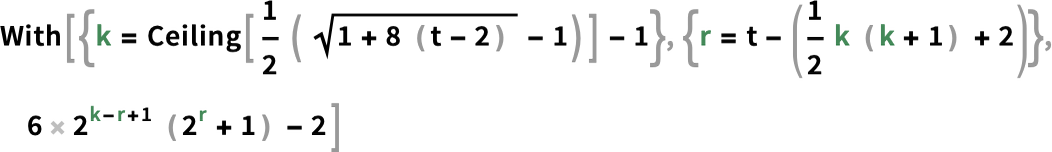
And, yes, it’s quite remarkable that these formulas exist, yet are as comparatively complicated as they are. In effect, they’re taking us a certain distance to the edge of what can be captured with traditional mathematics, as opposed to being findable only by irreducible computation.
The World of Larger Lambdas
We’ve looked systematically at lambdas up to size 8. So what happens with larger lambdas?
Size 9
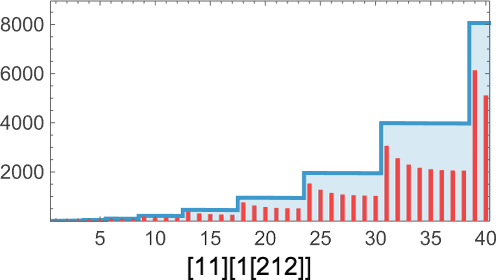
At size 9 there are 454,283 possible lambdas. Now the distribution of lifetimes is:
The longest finite lifetime—of 55 steps—occurs for
which eventually evolves to just:
Here are the sizes of the lambdas obtained at each step:
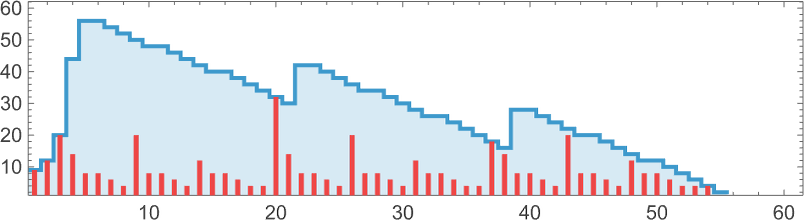
But why does this particular process terminate? It’s not easy to see. Looking at the sequence of trees generated, there’s some indication of how branches rearrange and then disappear:
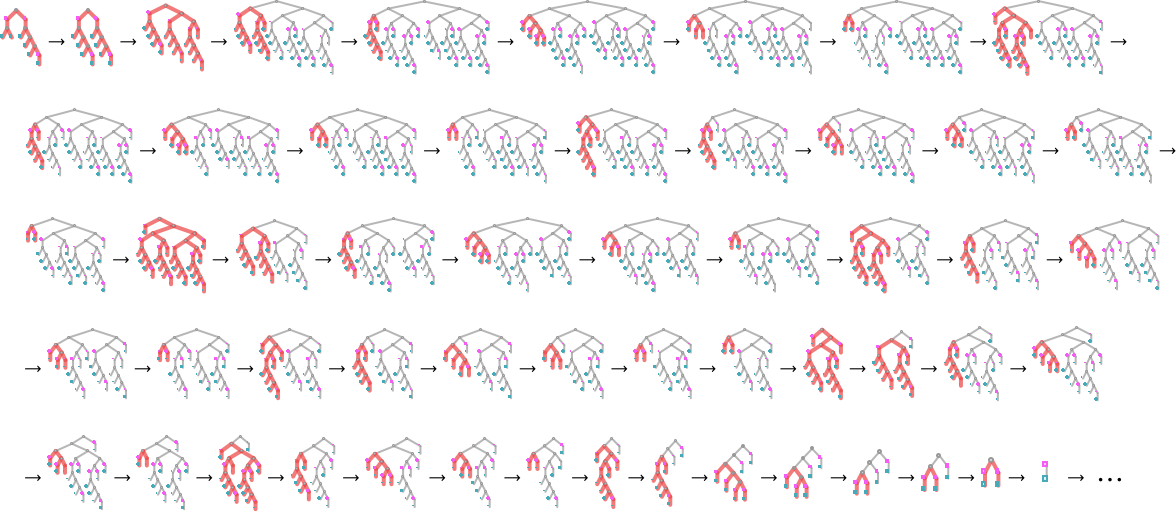
The array plot isn’t very illuminating either:
As is so often the case, it doesn’t seem as if there’s any “identifiable mechanism” to what happens; it “just does”.
The runner-up for lifetime among length-9 lambdas—with lifetime 44—is
which eventually evolves to
(which happens to correspond to the integer 16 in the representation we discussed above):
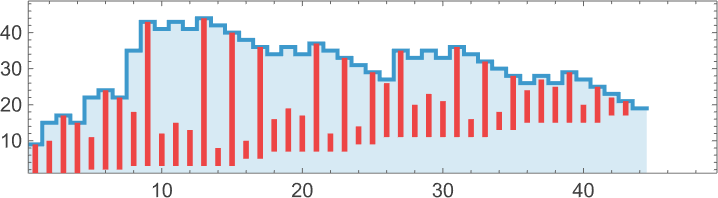
Viewed in “array” form, there’s at least a hint of “mechanism”: we see that over the course of the evolution there’s a steady (linear) increase in the quantity of “pure applications” without any λ’s to “drive things”:
Of the 748 size-9 lambdas that grow forever, most have ultimately periodic patterns of growth. The one with the longest growth period (10 steps) is
which has a rather unremarkable pattern of growth:
Only 35 lambdas have more complicated patterns of growth:
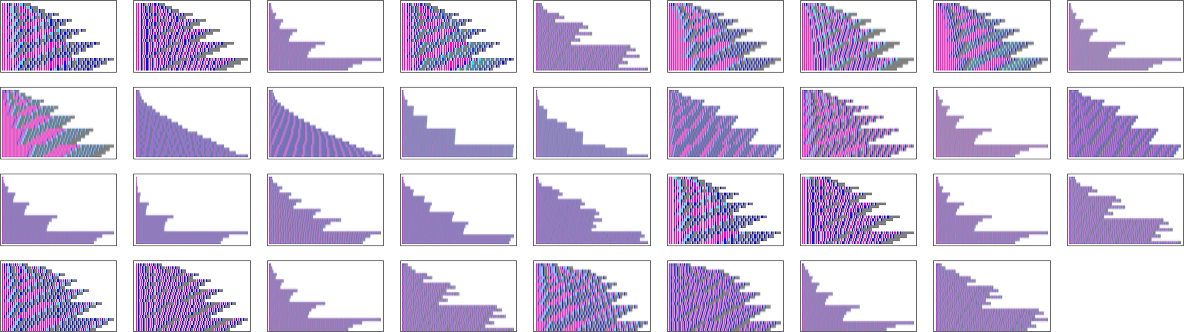
Many have behavior similar to what we saw with size 8. There can be nested patterns of growth, with an envelope that’s linear:
There can be what’s ultimately pure exponential 
growth:
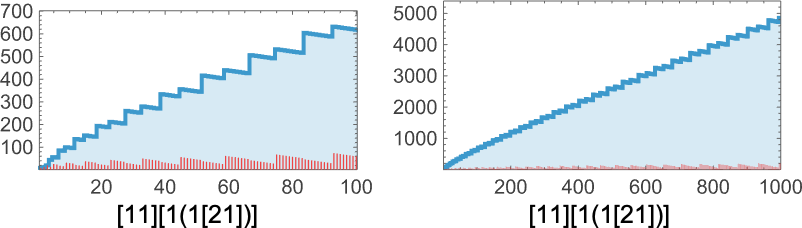
There can also be slower but still exponential growth, in this case 
:
There’s growth that at first looks like it might be complicated, but eventually ends up linear:
Then there’s what might seem to be irregular growth:
But taking differences reveals a nested structure
even though there’s no obvious nested structure in the detailed pattern of lambdas in this case:
And that’s about it for size 9.
Size 10
OK, what about size 10? There are now 5,159,441 possible lambdas. Of these, 38% are inert and 0.15% of them don’t terminate. The distribution of lifetimes is:
Some examples of lambdas with long lifetimes are:
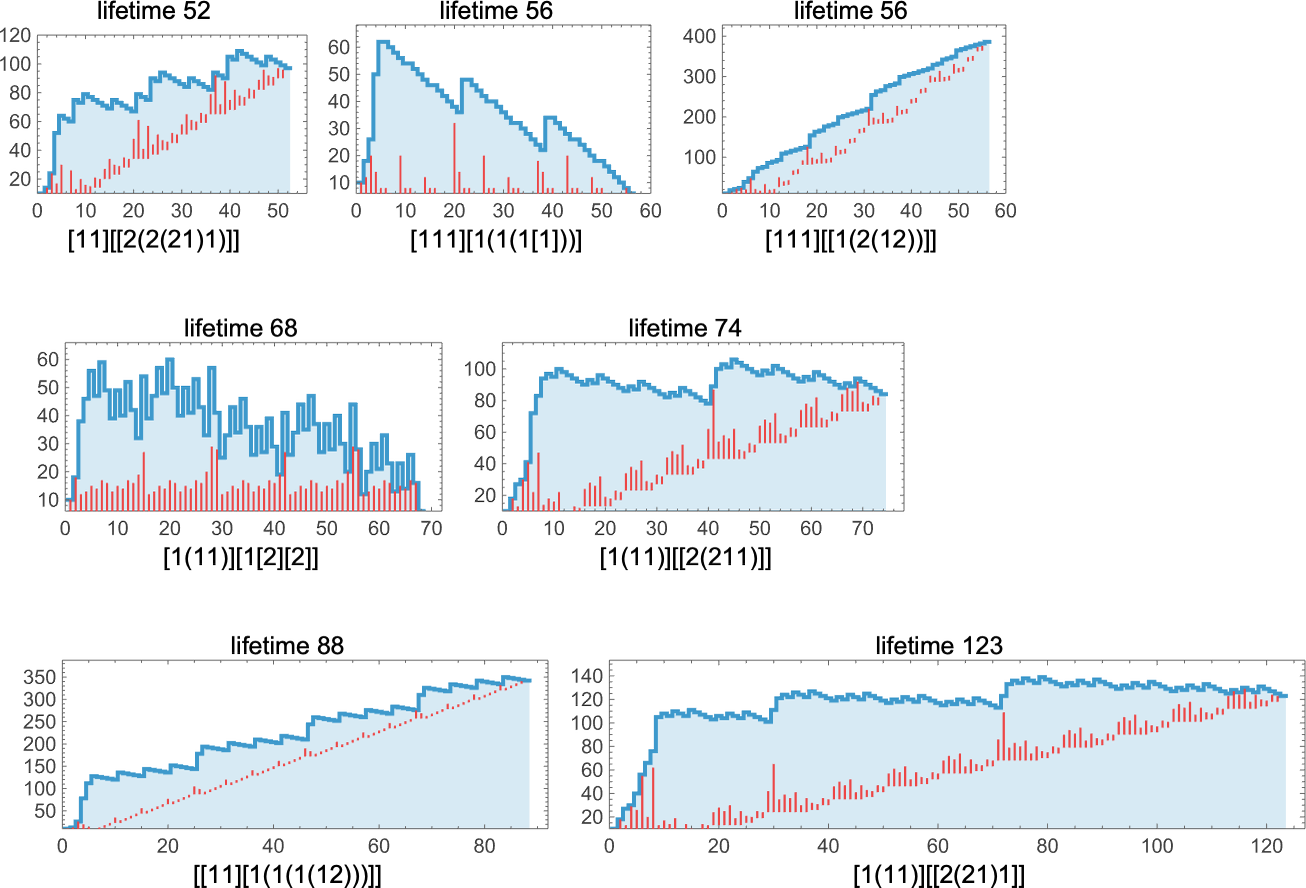
Some of these terminate with small lambdas; the one with lifetime 88 yields a lambda of size 342, while the second one with lifetime 56 yields one of size 386:
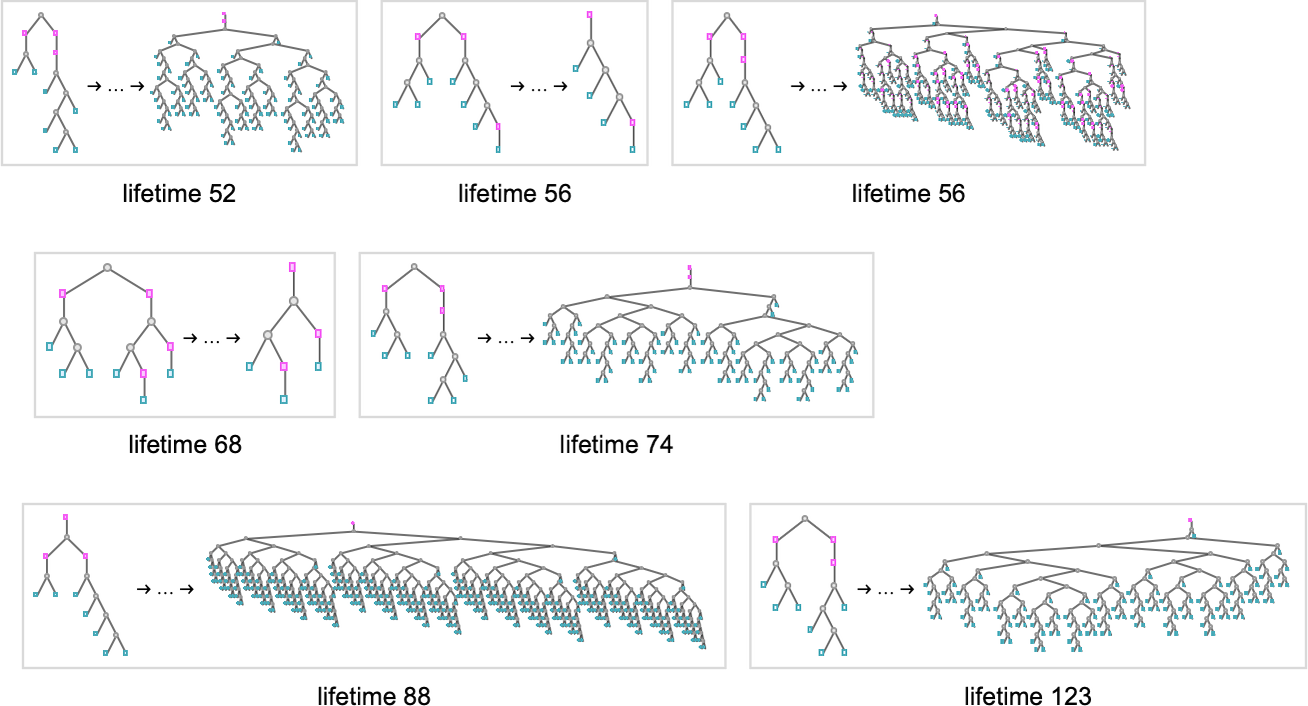
All of these work in somewhat different ways. In some cases the behavior looks quite systematic, and it’s at least somewhat clear they’ll eventually halt; in others it’s not at all obvious:
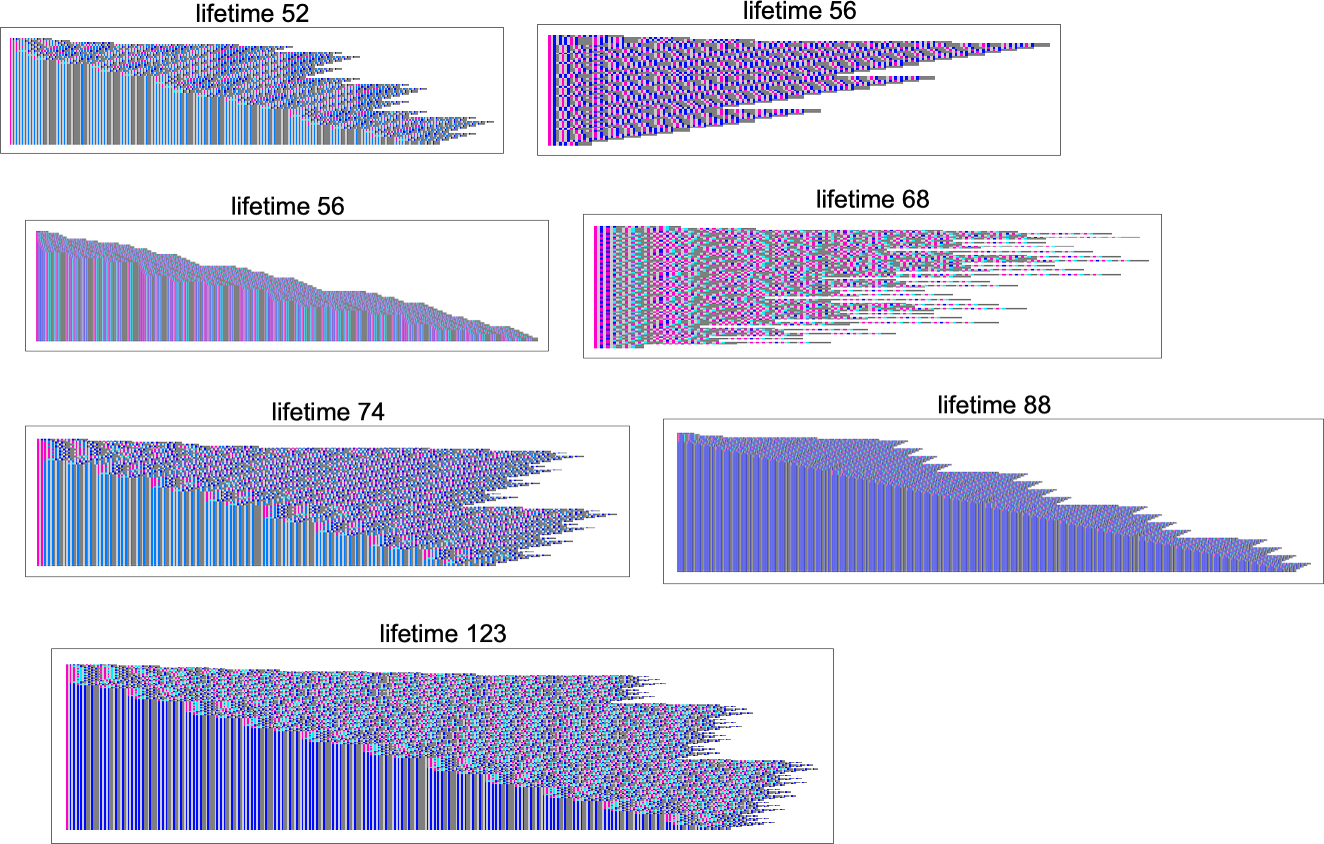
It’s notable that many, though not all, of these evolutions show linearly increasing “dead” regions, consisting purely of applications, without any actual λ’s—so that, for example, the final fixed point in the lifetime-123 case is:
What about other cases? Well, there are surprises. Like consider:
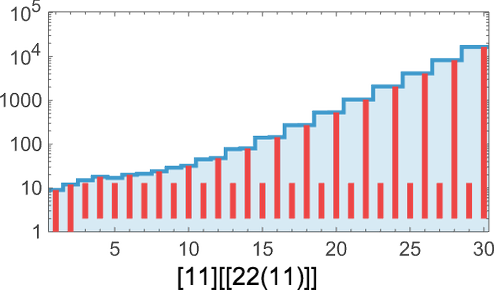
Running this, say, for 2000 steps it seems to be just uniformly growing:
But then, suddenly, after 3779 steps, there’s a surprise: it terminates—leaving a lambda of size 4950:
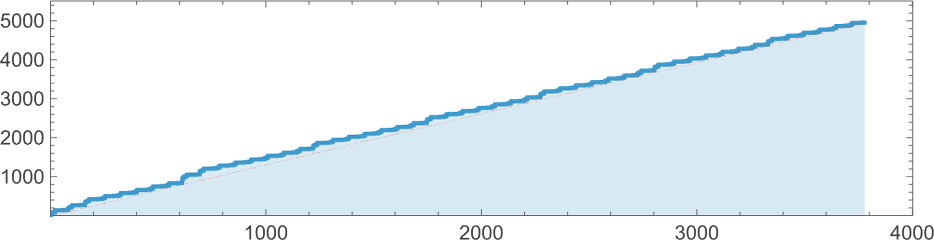
Looking at successive size differences doesn’t give any obvious “advance warning” of termination:
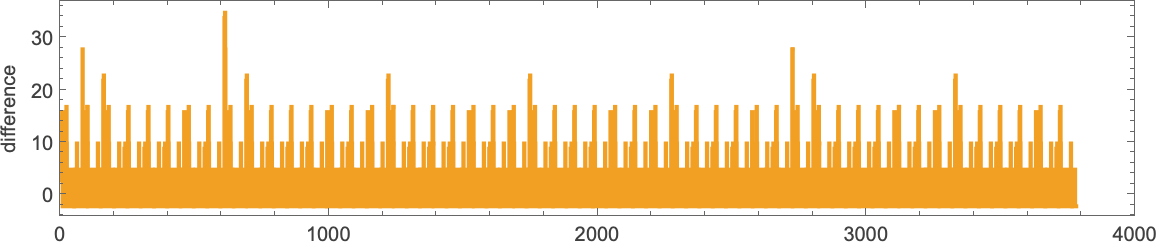
But if one looks at the actual sequence of lambdas generated (here just for 200 steps) we see what appears to be a somewhat telltale buildup of “dead” applications:
And, indeed, in the next section, we’ll see an even longer-lived example.
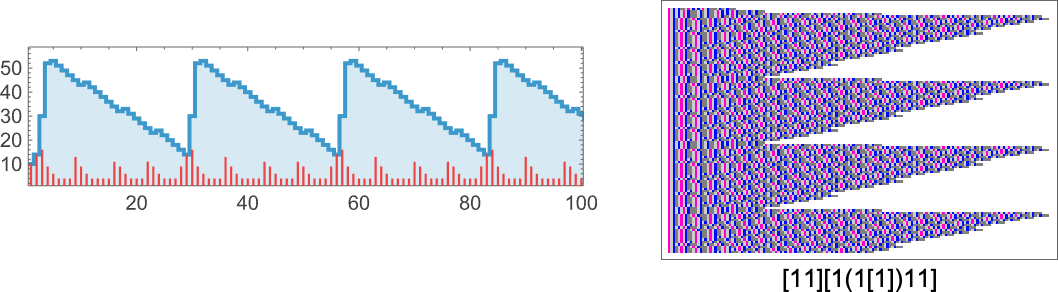
Even though it’s sometimes had to tell whether the evaluation of a lambda will terminate, there are plenty of cases where it’s obvious. An example is when the evaluation chain ultimately becomes periodic. At size 10, there are longer periods than before; here’s an example with period 27:
There’s also growth where the sequence of sizes has obvious nested structure—with a linearly growing envelope:
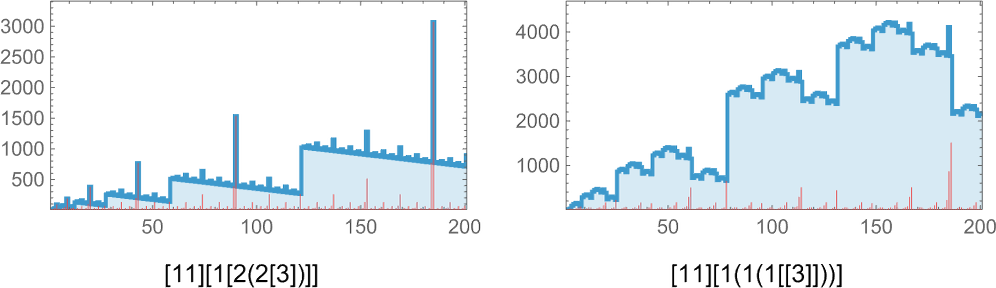
And then there’s nested structure, but superimposed on 
growth:
Size 11
At size 11, there are 63,782,411 possible lambdas. Most of the behavior one sees looks very much as before. But there are some surprises. One of them is:
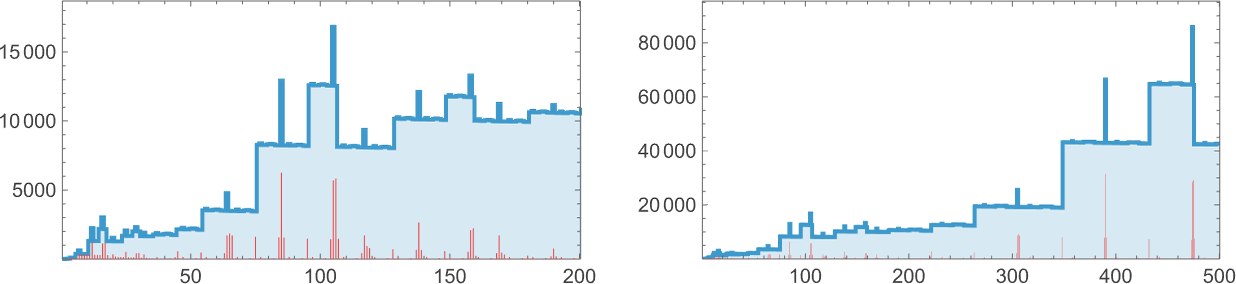
And another is:
And, yes, there doesn’t seem to be any overall regularity here, and nor does any show up in the detailed sequence of lambdas produced:
So far as I can tell, like so many other simple computational systems—from rule 30 on—the fairly simple lambda
just keeps generating unpredictable behavior forever.
The Issue of Undecidability
How do we know whether the evaluation chain for a particular lambda will terminate? Well, we can just run for a certain number of steps and see if it terminates by then. And perhaps by that point we will see obvious periodic or nested behavior that will make it clear that it won’t ever terminate. But in general we have no way to know how long we might have to run it to be able to determine whether it terminates or not.
It’s a very typical example of the computational irreducibility that occurs throughout the world of even simple computational systems. And in general it leads us to say that the problem of whether a given lambda evaluation will terminate must be considered undecidable, in the sense that there’s no computation of bounded length that can guarantee to answer the question.
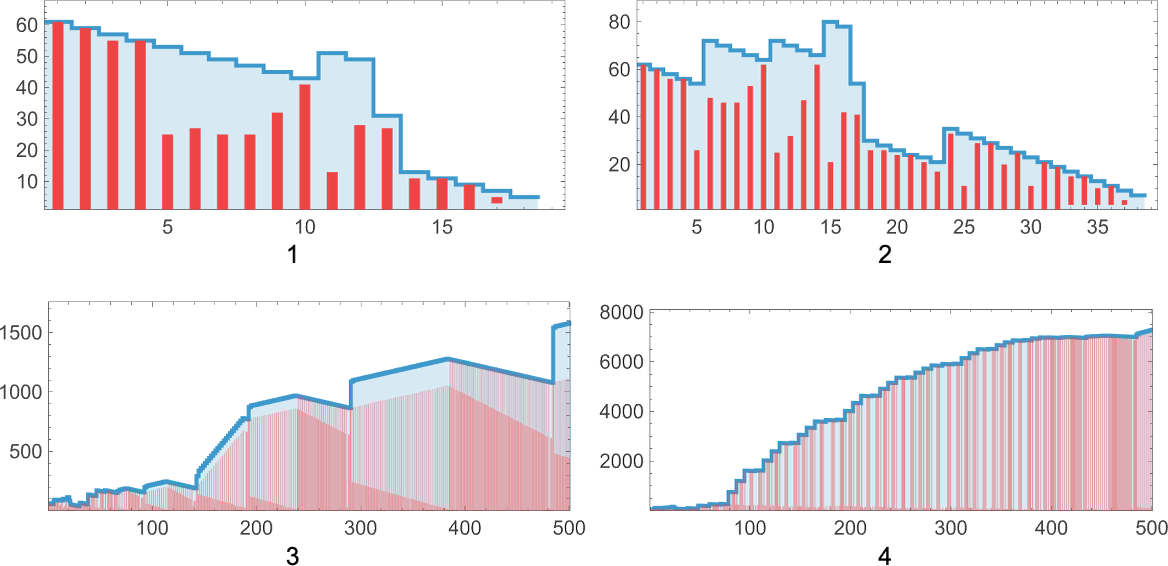
But what happens in practice? Well, we’ve seen above that at least for sufficiently small lambdas it’s not too hard to resolve the question of termination. But already at size 10 there are issues. Take for example:
The first 1000 steps of evaluation lead to lambdas with a sequence of sizes that seem like they’re basically just uniformly increasing:
After 10,000 steps it’s the same story—with the size growing roughly like 
:
But if we look at the structure of the actual underlying lambdas—even for just 200 steps—we see that there’s a “dead region” that’s beginning to build up:
Continuing to 500 steps, the dead region continues to grow more or less linearly:
“Detrending” the sequences of sizes by subtracting 
we get:
There’s definite regularity here, which suggests that we might actually be able to identify a “pocket of computational reducibility” in this particular case—and be able to work out what will happen without having to explicitly run each step.
And, yes, in fact that’s true. Let’s look again at the form of the lambda we’re dealing with:
The second part turns out to be the (“Church numeral”) representation we used for the number 2. Calling
this 
the whole lambda
evaluates according to:
Normally you might think of doing things like arithmetic operations on integers. But here we’re seeing something different: we’re seeing integers in effect applied to integers. So what, for example, does
or
evaluate to? Repeatedly doing beta reduction gives:
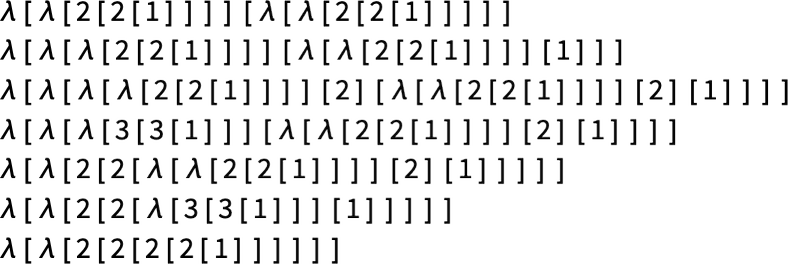
Or, in other words 
gives 
. Here are some
other examples:
And in general:
So now we can “decode” our original lambda. Since
evaluates to
this means that
is just:
Or, in other words, despite how it might have looked at first, the evaluation of our original lambda will
eventually terminate, giving a lambda of size 65539—and it’ll take about 200,000 steps to do this.
(Curiously, this whole setup is extremely similar to something I studied about 30 years
ago in connection with combinator-like systems of the form e[x_][y_]
x[x[y]].)
It’s somewhat remarkable how long it took our simple lambda to terminate. And actually, given what we’ve seen here, it’s straightforward to construct lambdas that will terminate, but will take even longer to do so. So, for example
evaluates to the n-fold “tetration”
and takes about that many steps to do so.
In the next section we’ll see how to set up lambdas that can compute not just tetration, but the Ackermann function, and any level of hyperoperation, as defined recursively by
(where h[1] is Plus, h[2] is Times, h[3] is Power, h[4] is tetration, etc.).
OK, so there are lambdas (and actually even rather simple ones) whose evaluation terminates, but only after a number of steps that has to be described with hyperoperations. But what about lambdas that don’t terminate at all? We can’t explicitly trace what the lambda does over the course of an infinite number of steps. So how can we be sure that a lambda won’t terminate?
Well, we have to construct a proof. Sometimes that’s pretty straightforward because we can easily identify that something fundamentally simple is going on inside the lambda. Consider for example:
The successive steps in its evaluation are (with the elements involved in each beta reduction highlighted):
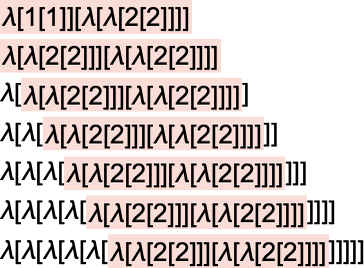
It’s very obvious what’s going on here, and that it will continue forever. But if we wanted to, we could construct a formal proof of what’s going to happen—say using mathematical induction to relate one step to the next.
And indeed whenever we can identify a (“stem-cell-like”) core “generator” that repeats, we can expect to be able to use induction to prove that there won’t be termination. There are also plenty of other cases that we’ve seen in which we can tell there’s enough regularity—say in the pattern of successive lambdas—that it’s “visually obvious” there won’t be termination. And though there will often be many details to wrestle with, one can expect a straightforward path in such cases to a formal proof based on mathematical induction.
In practice one reason “visual obviousness” can sometimes be difficult to identify is that lambdas can grow too fast to be consistently visualized. The basic source of such rapid growth is that beta reduction ends up repeatedly replicating increasingly large subexpressions. If these replications in some sense form a simple tree, then one can again expect to do induction-based proofs (typically based on various kinds of tree traversals). But things can get more complicated if one starts ascending the hierarchy of hyperoperations, as we know lambdas can. And for example, one can end up with situations where every leaf of every tree is spawning a new tree.
At the outset, it’s certainly not self-evident that the process of induction would be a valid way to construct a proof of a “statement about infinity” (such as that a particular lambda won’t ever terminate, even after an infinite number of steps). But induction has a long history of use in mathematics, and for more than a century has been enshrined as an axiom in Peano arithmetic—the axiom system that’s essentially universally used (at least in principle) in basic mathematics. Induction in a sense says that if you always have a way to take a next step in a sequence (say on a number line of integers), then you’ll be able to go even infinitely far in that sequence. But what if what you’re dealing with can’t readily be “unrolled” into a simple (integer-like) sequence? For example, what if you’re dealing with trees that are growing new trees everywhere? Well, then ordinary induction won’t be enough to “get you to all the leaves”.
But in set theory (which is typically the ultimate axiom system in principle used for current mathematics) there are axioms that go beyond ordinary induction, and that allow the concept of transfinite induction. And with transfinite induction (which can “walk through” all possible ordered sets) one can “reach the leaves” in a “trees always beget trees” system.
So what this means is that while the nontermination of a sufficiently fast-growing lambda may not be something that can be proved in Peano arithmetic (i.e. with ordinary induction) it’s still possible that it’ll be provable in set theory. Inevitably, though, even set theory will be limited, and there’ll be lambdas whose nontermination it can’t prove, and for which one will have to introduce new axioms to be able to produce a proof.
But can we explicitly see lambdas that have these issues? I wouldn’t be surprised if some of the ones we’ve already considered here might actually be examples. But that will most likely be a very difficult thing to prove. And an easier (but still difficult) approach is to explicitly construct, say, a family of lambdas where within Peano arithmetic there can be no proof that they all terminate.
Consider the slightly complicated definitions:
The 
are the so-called Goodstein
sequences for which it’s known that the statement that they always reach 0 is one that can’t be
proved purely using ordinary induction, i.e. in Peano arithmetic.
Well, here’s a lambda—that’s even comparatively simple—that has been constructed to compute the lengths of the Goodstein sequences:
Feed in a representation of an integer n, and this lambda will compute a representation of the
length of the corresponding sequence 
(i.e. how many terms are needed to reach 0). And this length will be finite if (and only if) the
evaluation of the lambda terminates. So, in other words, the statement that all lambda evaluations of
this kind terminate is equivalent to the statement that all Goodstein sequences eventually reach 0.
But what actually happens if we evaluate lambdas of this kind? Here are the results for the first few
values of 
:
For 
, the process terminates in 18 steps with final result
λ[λ[2[2[1]]]]—our representation for the integer 2— reflecting the fact that 
. For 
, after 38 steps we get the integer 4, reflecting the fact that 
. For 
many more steps are needed, but eventually the
result is 6 (reflecting the fact that 
). But what about 
? Well, it’s known that the process must
eventually terminate in this case too. But it must take a very long time—since the final result is known
to be 
. And if we keep going, the sizes—and
corresponding times—rapidly get still much, much larger.
This certainly isn’t the only way to “escape provability by Peano arithmetic”, but it’s an example of what this can look like.
We should remember that in general whether the evaluation of a lambda ever terminates is a question that’s fundamentally undecidable—in the sense that no finite computation whatsoever can guarantee to answer it. But the question of proving, say, that the evaluation of a particular lambda doesn’t terminate is something different. If the lambda “wasn’t generating much novelty” in its infinite lifetime (say it was just behaving in a repetitive way) then we’d be able to give a fairly simple proof of its nontermination. But the more fundamentally diverse what the lambda does, the more complicated the proof will be. And the point is that—essentially as a result of computational irreducibility—there must be lambdas whose behavior is arbitrarily complex, and diverse. But in some sense any given finite axiom system can only be expected to capture a certain “level of diversity” and therefore be able to prove nontermination only for a certain set of lambdas.
To be slightly more concrete, we can imagine a construction that will lead us to a lambda whose termination can’t be proved within a given axiom system. It starts from the fact that the computation universality of lambdas implies that any computation can be encoded as the evaluation of some lambda. So in particular there’s a lambda that systematically generates statements in the language of a given axiom system, determining whether each of those statements is a theorem in that axiom system. And we can then set it up so that if ever an inconsistency is found—in the sense that both a theorem and its negation appear—then the process will stop. In other words, the evaluation of the lambda is in a sense systematically looking for inconsistencies in the axiom system, terminating if it ever finds one.
So this means that proving the evaluation of the lambda will never terminate is equivalent to proving that the axiom system is consistent. But it’s a fundamental fact that a given axiom system can never prove its own consistency; it takes a more powerful axiom system to do that. So this means that we’ll never be able to prove that the evaluation of the lambda we’ve set up terminates—at least from within the axiom system that it’s based on.
In effect what’s happened is that we’ve managed to make our lambda in its infinite lifetime scan through everything our axiom system can do, with the result that the axiom system can’t “go further” and say anything “bigger” about what the lambda does. It’s a consequence of the computation universality of lambdas that it’s possible to package up the whole “metamathematics” of our axiom system into the (infinite) behavior of a single lambda. But the result is that for any given axiom system we can in principle produce a lambda where we know that the nontermination of that lambda is unprovable within that axiom system.
Of course, if we extend our axiom system to have the additional axiom “this particular lambda never terminates” then we’ll trivially be able to prove nontermination. But the underlying computation universality of lambdas implies (in an analog of Gödel’s theorem) that no finite collection of axioms can ever successfully let us get finite proofs for all possible lambdas.
And, yes, while the construction we’ve outlined gives us a particular way to come up with lambdas that “escape” a given axiom system, those certainly won’t be the only lambdas that can do it. What will be the smallest lambda whose nontermination is unprovable in, say, Peano arithmetic? The example we gave above based on Goodstein sequences is already quite small. But there are no doubt still much smaller examples. Though in general there’s no upper bound on how difficult it might be to prove that a particular lambda is indeed an example.
If we scan through all possible lambdas, it’s inevitable that we’ll eventually find a lambda that can “escape” from any possible axiom system. And from experience in the computational universe, we can expect that even for quite small lambdas there’ll be rapid acceleration in the size and power of axiom systems needed to “rein them in”. Yes, in principle we can just add a custom axiom to handle any given lambda, but the point is that we can expect that there’ll quickly be in a sense “arbitrarily small leverage”: each axiom added will cover only a vanishingly small fraction of the lambdas we reach.
Numerically Interpretable Lambdas
So far, we’ve discussed the evaluation of “lambdas on their own”. But given a particular lambda, we can always apply it to “input”, and see “what it computes”. Of course, the input itself is just another lambda, so a “lambda applied to input” is just a “lambda applied to a lambda”, which is itself a lambda. And so we’re basically back to looking at “lambdas on their own”.
But what if the input we give is something “interpretable”? Say a lambda corresponding to an integer in the representation we used above. A lambda applied to such a thing will—assuming it terminates—inevitably just give another lambda. And most of the time that resulting lambda won’t be “interpretable”. But sometimes it can be.
Consider for example:
Here’s what happens if we apply this lambda to a sequence of integers represented as lambdas:
In other words, this lambda can be interpreted as implementing a numerical function from integers to integers—in this case the function:
So what kinds of such numerical functions can lambdas represent? Insofar as lambdas are capable of universal computation, they must in the end be capable of representing any integer function. But the necessary lambda could be very large.
Early on above, we saw a constructed representation for the factorial function as a lambda:
We also know that if we take the (“Church numeral”) lambda that represents an integer m and apply it to the lambda that represents n, we get the lambda representing nm. It’s then straightforward to construct a lambda that represents any function that can be obtained as a composition of powers:
And one can readily go on to get functions based on tetration and higher hyperoperations. For example
gives a diagonal of the Ackermann function whose successive terms are:
But what about “lambdas in the wild”? How often will they be “numerically interpretable”? And what kinds of functions will they represent? Among size-5 lambdas, for example, 10 out of 82—or about 12%—are “interpretable”, and represent the functions 0, 1, n and n2. Among size-10 lambdas the fraction that are “interpretable” falls to about 4%, and the frequency with which different functions occur is:
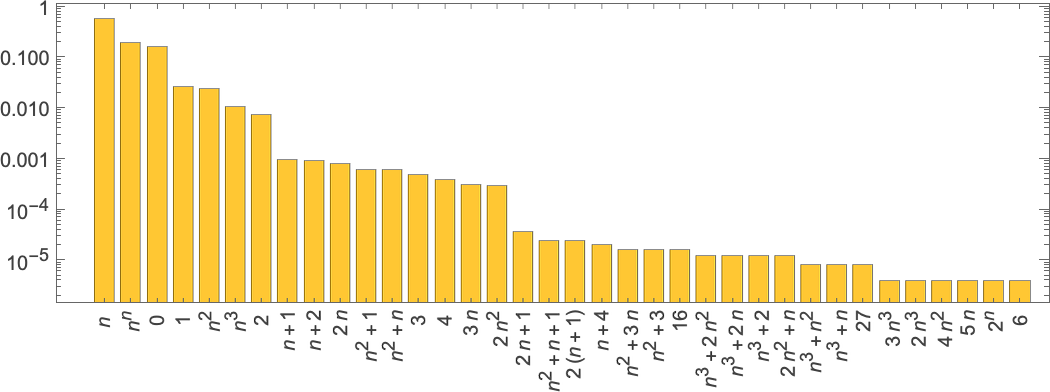
Looking at lambdas of successively greater size, here are some notable “firsts” of where functions appear:
And, yes, we can think of the size of the minimal lambda that gives a particular function to be the “algorithmic information content” of that function with respect to lambdas.
Needless to say, there are some other surprises. Like
, which gives 0 when fed any integer as input, but takes a
superexponentially increasing number of steps to do so:
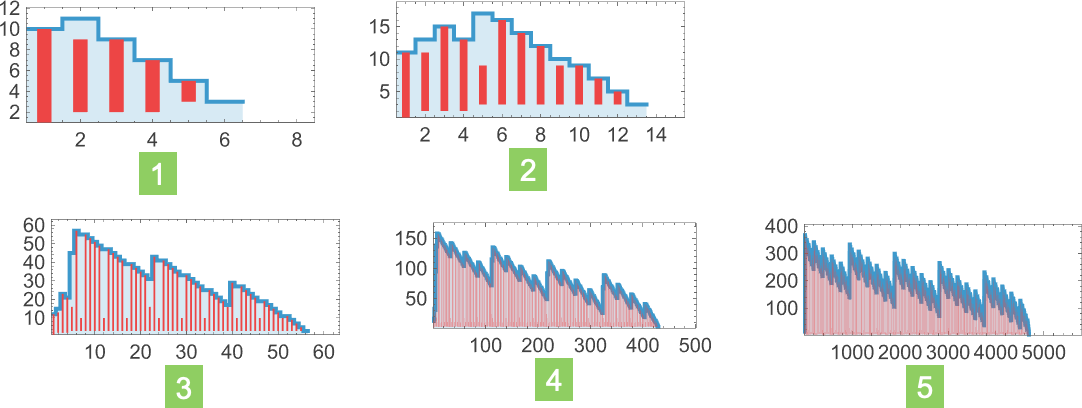
We’ve been discussing what “numerical” functions can be computed by what lambdas. But another question we can ask is how much time (i.e. how many beta reductions) such computations will take—or how much “space” they’ll need for intermediate expressions. And indeed, even if the outputs are the same, different lambdas can take different computational approaches and different computational resources to reach those outputs. So, for example, among size-8 lambdas, there are 41 that compute the function n2. And here are the sizes of intermediate expressions (all plotted on the same scale) generated by running these lambdas for the case n = 10:
The pictures suggest that these various lambdas have a variety of different approaches to computing n2. And some of these approaches take more “memory” (i.e. size of intermediate lambdas) than others. And in addition some take more time than others.
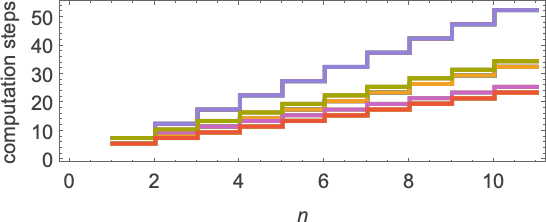
For this particular set of lambdas, the time required always grows essentially just linearly with n, though at several different possible rates:
But in other cases, different behavior is observed, including some very long “run times”. And indeed, in general, one can imagine building up a whole computational complexity theory for lambdas, starting with these kinds of empirical, ruliological investigations.
Everything we’ve discussed here so far is for functions with single arguments. But we can also look at
functions that have multiple arguments, which can be fed to lambdas in “curried” form: f
[x][y], etc. And with this setup,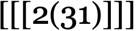
, for example, gives x y while
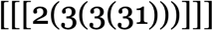gives x y3.
Multiway Graphs for Lambda Evaluation
Let’s say you’re evaluating a lambda expression like:
You want to do a beta reduction. But which one? For this expression, there are 3 possible places where a beta reduction can be done, all giving different results:
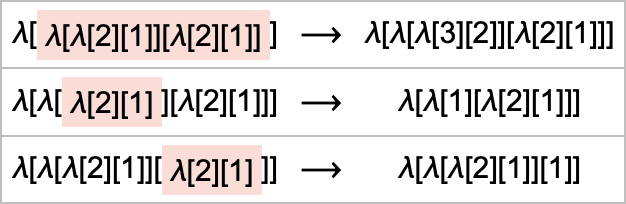
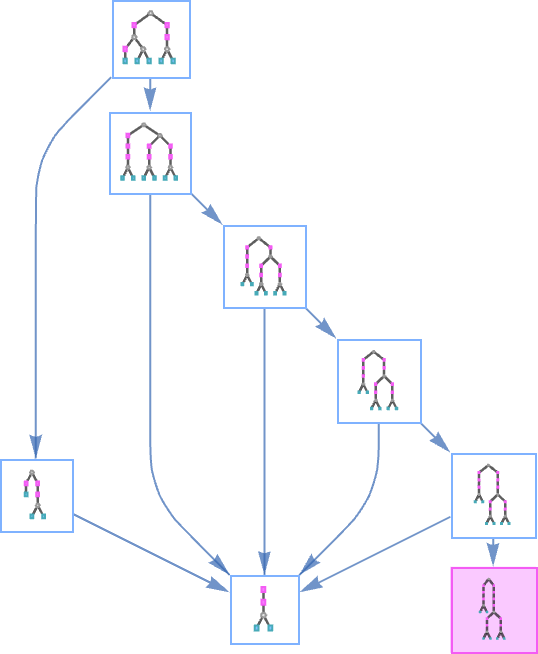
In everything we’ve done so far, we’ve always assumed that we use the “first” beta reduction at each step (we’ll discuss what we mean by “first” in a moment). But in general we can look at all possible “paths of evaluation”—and form a multiway graph from them (the double edge reflects the fact that two different beta reductions happen to both yield the same result):
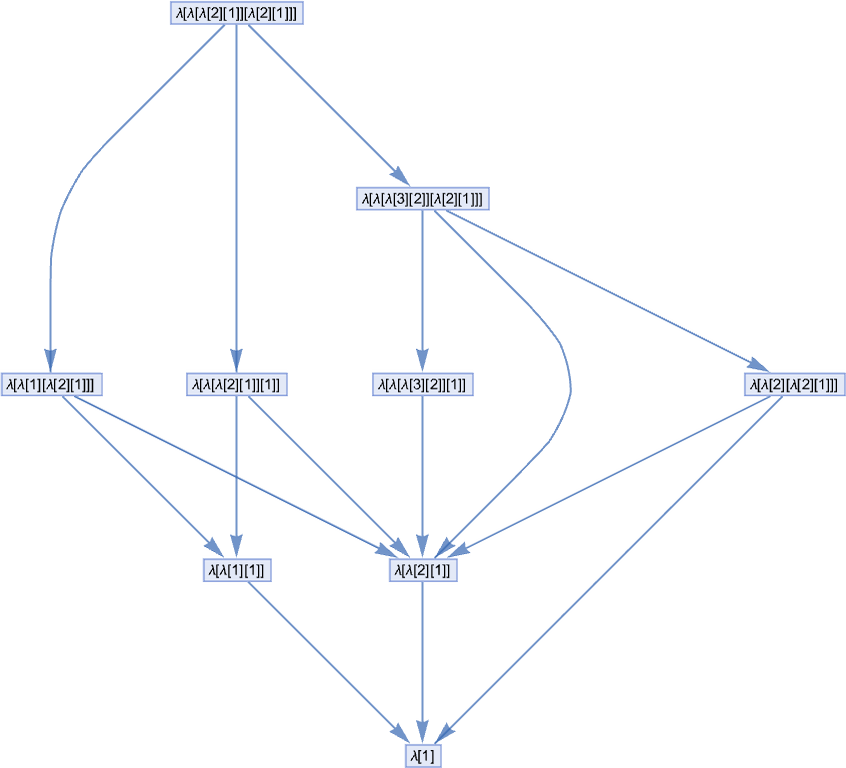
Our standard evaluation path in this case is then:
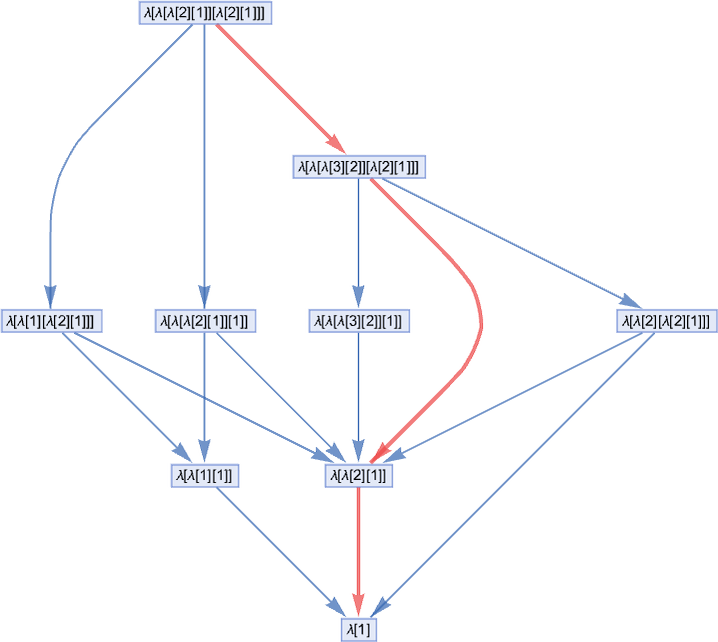
And we get this path by picking at each step the “leftmost outermost” possible beta reduction, i.e. the one that involves the “highest” relevant λ in the expression tree (and the leftmost one if there’s a choice):
But in the multiway graph above it’s clear we could have picked any path, and still ended up at the same final result. And indeed it’s a general property of lambdas (the so-called confluence or Church–Rosser property) that all evaluations of a given lambda that terminate will terminate with the same result.
By the way, here’s what the multiway graph looks like with the lambdas rendered in tree form:
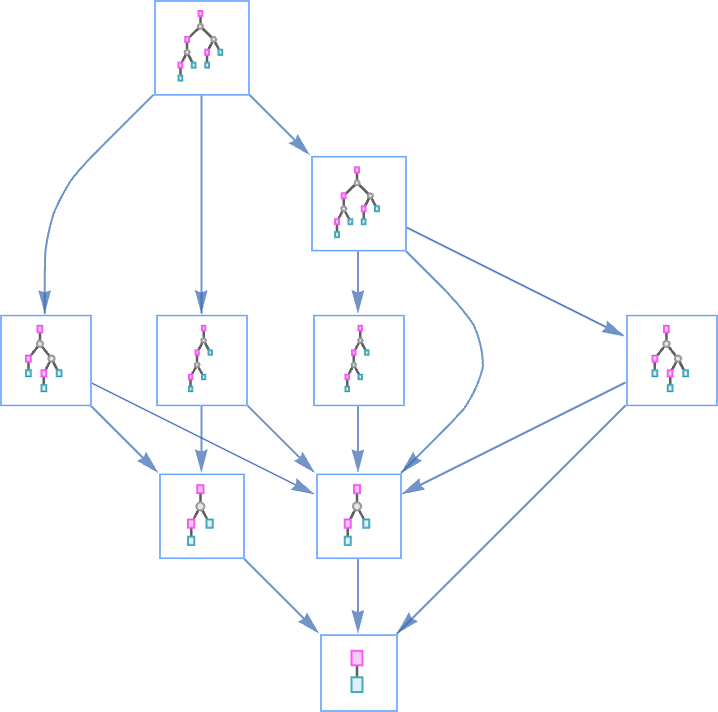
At size 5, all lambdas give trivial multiway graphs, that involve no branching, as in:
At size 6, there starts to be branching—and merging:
And something else happens too: the “looping lambda” λ[1[1]][λ[1[1]]] gives a multiway graph that is a loop:
At size 7 many distinct topologies of multiway graphs start to appear. Most always lead to termination:
(The largest of these multiway graphs is associated with λ[1[1]][λ[λ[2][1]]] and has 12 nodes.)
Then there are cases that loop:
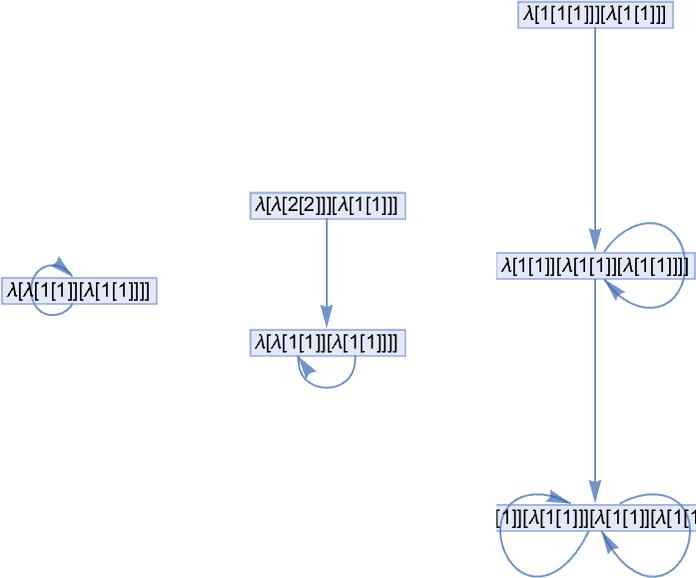
And finally there is
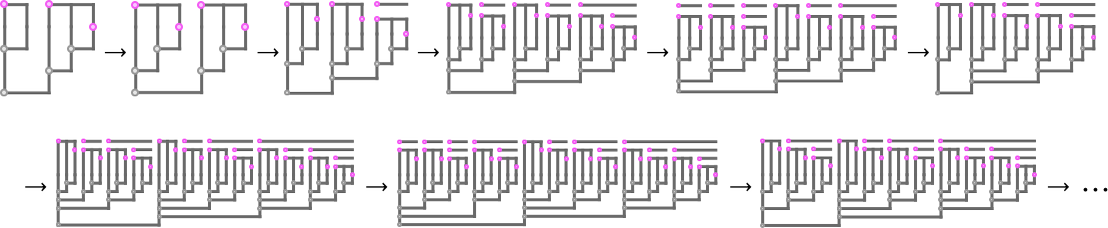
where something new happens: the multiway graph has many distinct branches. After 5 steps it is
where the size of each node indicates the size of the lambda it represents, and the pink nodes indicate lambdas that can be further beta reduced. After just one more step the multiway graph becomes
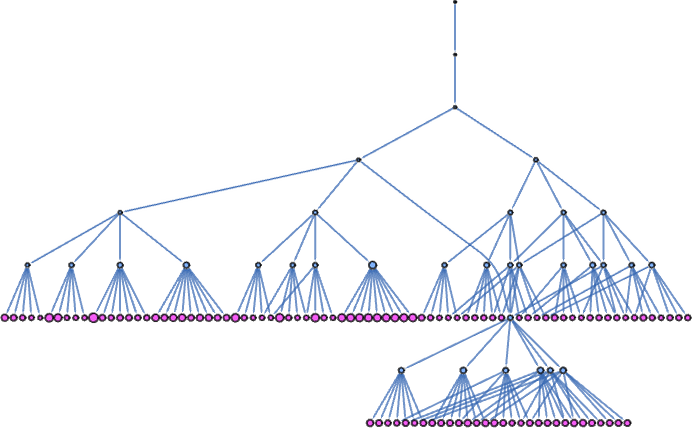
or, after another step, in a hyperbolic embedding:
In this particular case, no branch ever terminates, and the total size of the multiway system on successive steps is:
With size-8 lambdas, the terminating multiway graphs can be larger (the first case has 124 nodes):
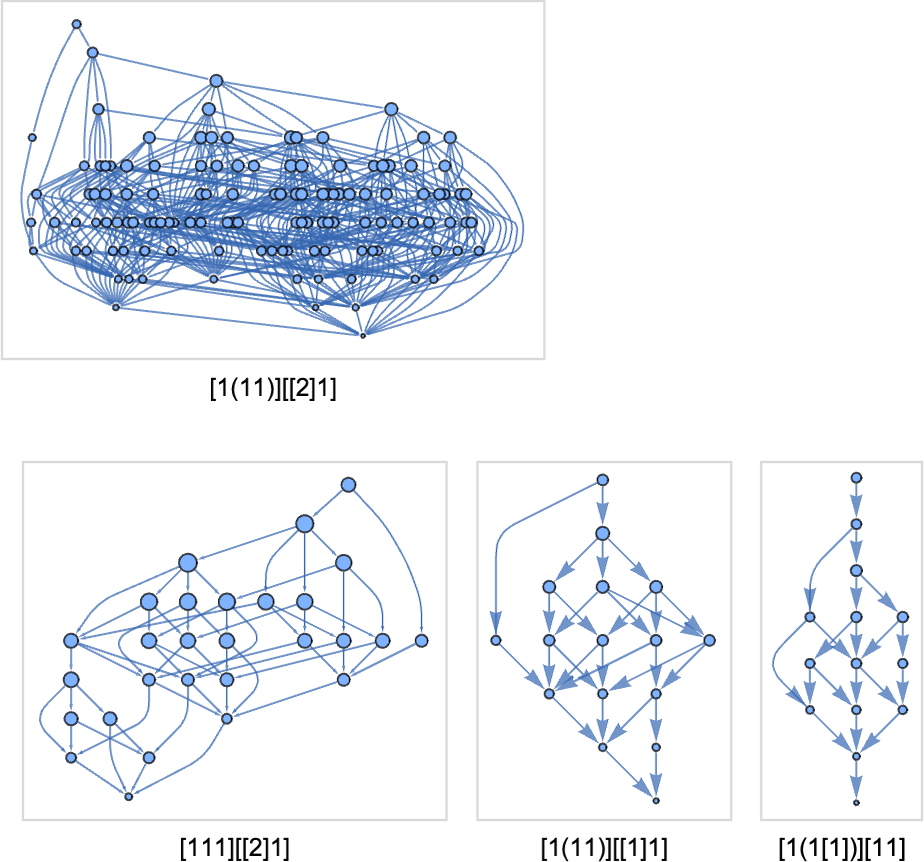
And there are all sorts of new topologies for nonterminating cases, such as:
These graphs are what one gets by doing 5 successive beta reductions. The ones that end in loops won’t change if we do more reductions. But the ones with nodes indicated in pink will. In most cases one ends up with a progressively increasing number of reductions that can be done (often exponential, but here just 2t – 1 at step t):
Meanwhile, sometimes, the number of “unresolved reductions” just remains constant:
We know that if there’s a fixed point to beta reductions, it’s always unique. But can there be both a unique fixed point, and branches that continue forever? It turns out that there can. And the first lambda for which this happens is:
With our standard evaluation method, this lambda terminates in 5 steps at λ[1]. But there are other paths that can be followed, that don’t terminate (as indicted by pink nodes at the end):
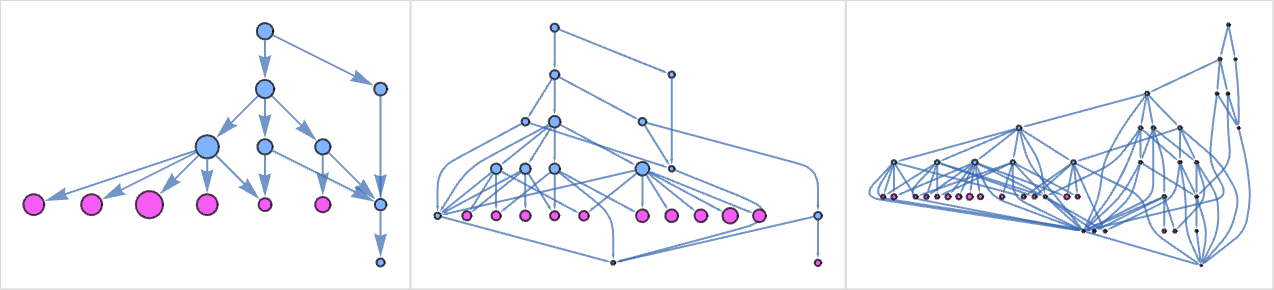
And indeed on step t, the number of such paths is given by a Fibonacci-like recurrence, growing
asymptotically 
.
With size-9 lambdas there’s a much simpler case where the termination/nontermination phenomenon occurs
where now at each step there’s just a single nonterminating path:
There’s another lambda where there’s alternation between one and two nonterminating paths:
And another where there are asymptotically always exactly 5 nonterminating paths:
OK, so some lambdas have very “bushy” (or infinite) multiway graphs, and some don’t. How does this correlate with the lifetimes we obtain for these lambdas through our standard evaluation process?
Here’s a plot of the size of the multiway graph versus lifetime for all finite-lifetime size-8 lambdas:
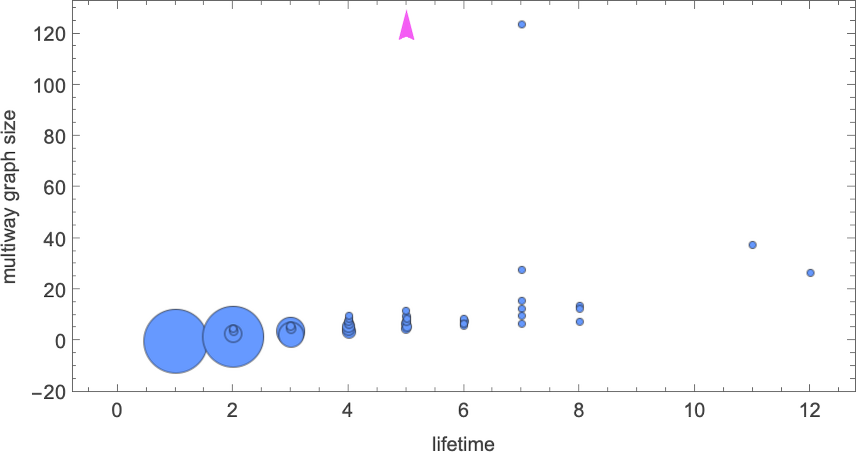
In all but the one case discussed above (and indicated here with a red arrow) the multiway graphs are of finite size—and we see some correlation between their size and the lifetime obtained with our standard evaluation process. Although it’s worth noting that even the lambda with the longest standard-evaluation lifetime (12) still has a fairly modest (27-node) multiway graph
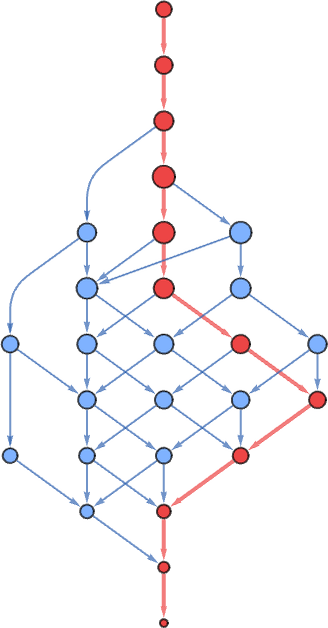
while the largest (finite) multiway graph (with 124 nodes) occurs for a lambda with standard-evaluation lifetime 7.
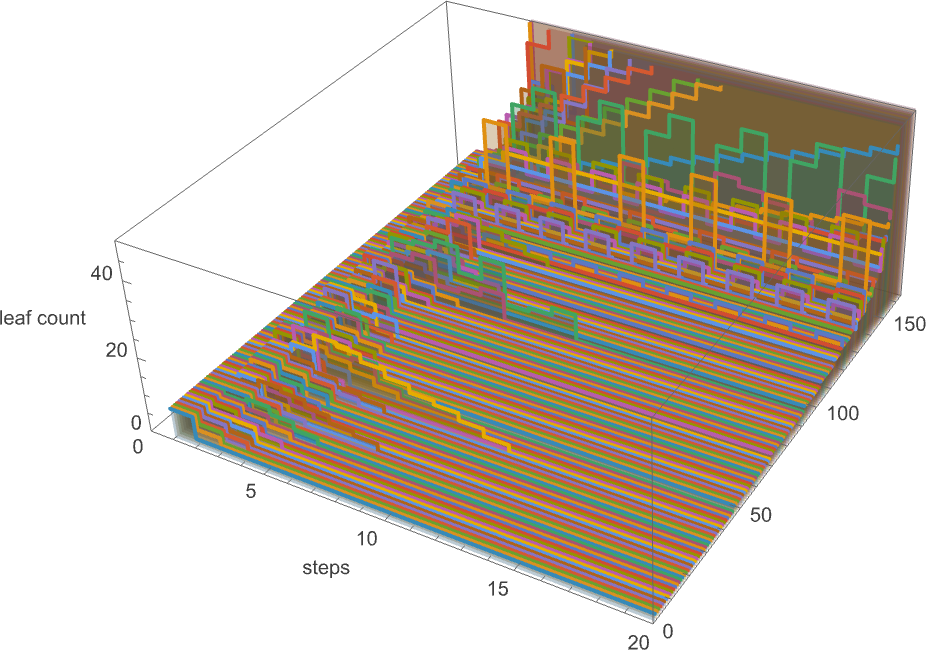
At size 9, here are the multiway graphs for the 10 lambdas with the longest standard-evaluation lifetimes, computed to 5 steps:
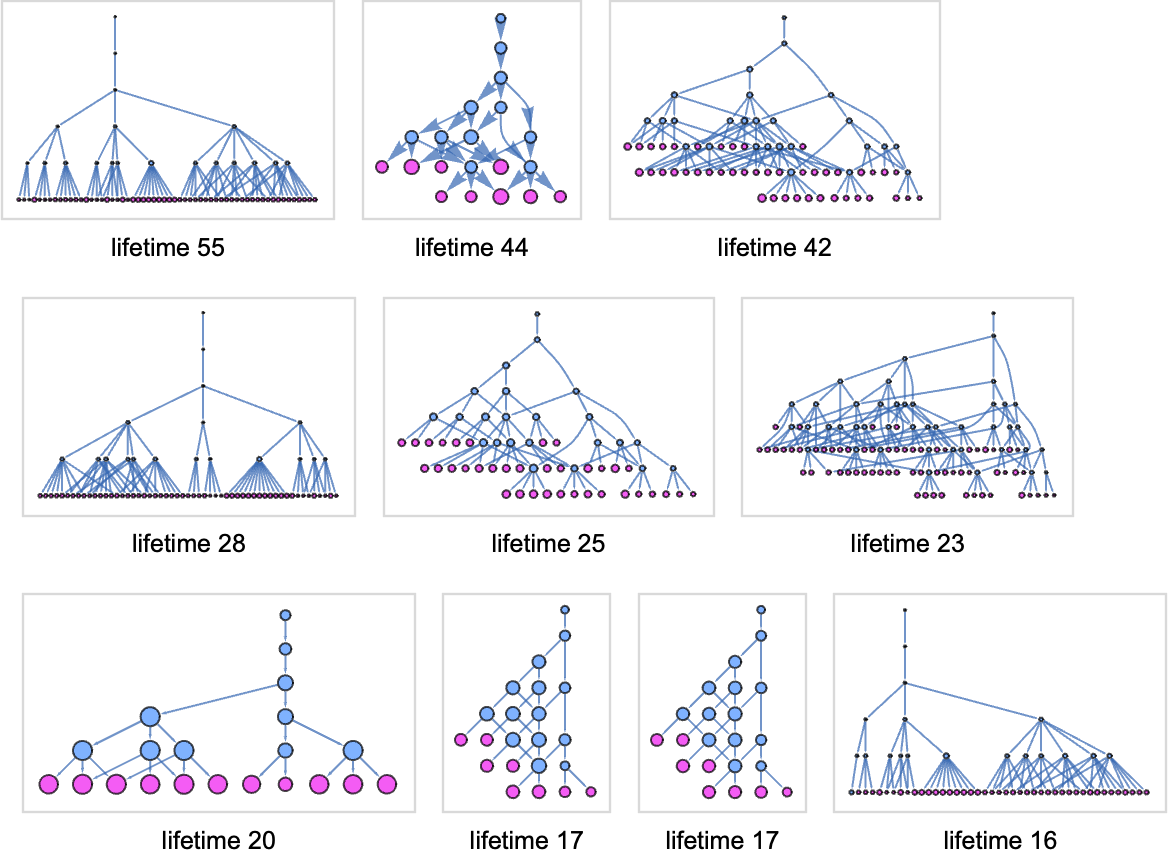
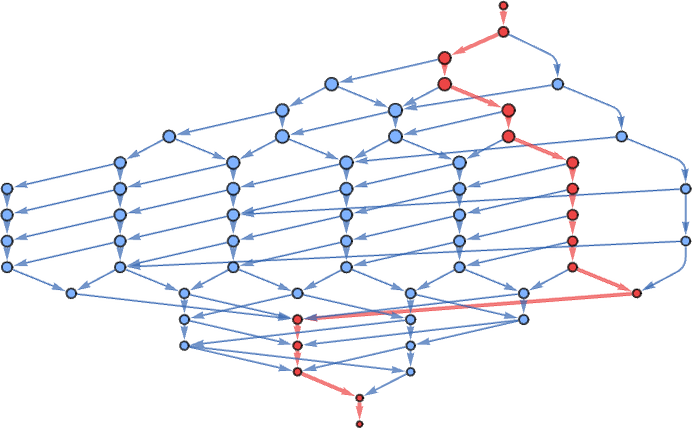
In the standard-evaluation lifetime-17 cases the multiway graph is finite:
But in all the other cases shown, the graph is presumably infinite. And for example, in the lifetime-55 case, the number of nodes at step t in the multiway graph grows like:
But somehow, among all these different paths, we know that there’s at least one that terminates—at least after 55 steps, to give λ[1].
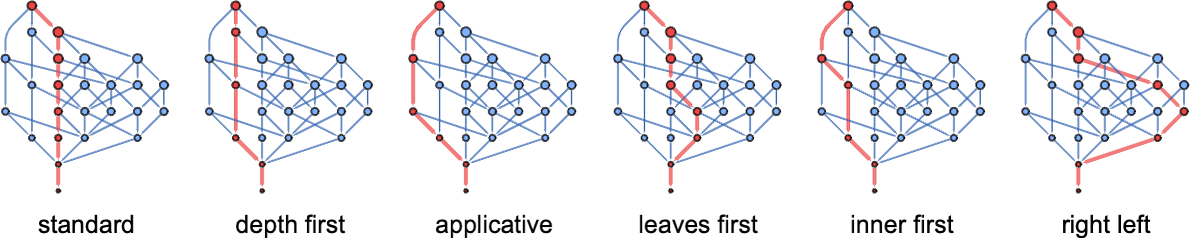
Different Evaluation Strategies
The multiway graph shows us all possible sequences of beta reductions for a lambda. Our “standard evaluation process” picks one particular sequence—by having a certain strategy for choosing at each step what beta reduction to do. But what if we were to use a different strategy?
As a first example, consider:
For this lambda, there turn out to be 4 possible positions at which beta reductions can be done (where the positions are specified here using Wolfram Language conventions):
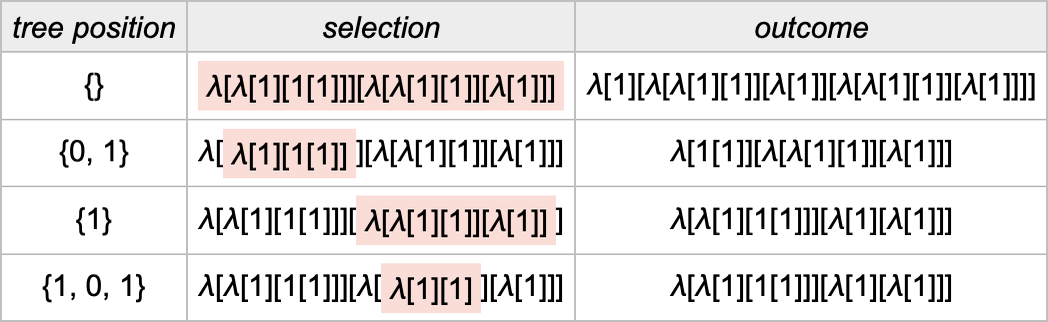
Our standard evaluation strategy does the beta reduction that’s listed first here. But how exactly does it determine that that’s the reduction it should do? Well, it looks at the lists of 0’s and 1’s that specify the positions of each of the possible reductions in the lambda expression tree. Then it picks the one with the shortest position list, sorting position lists lexicographically if there’s a tie.
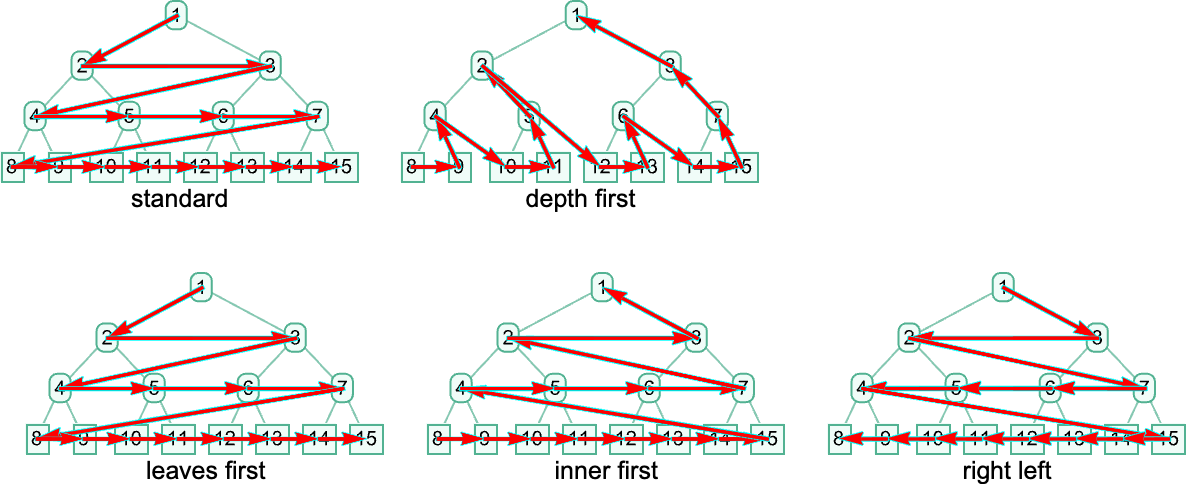
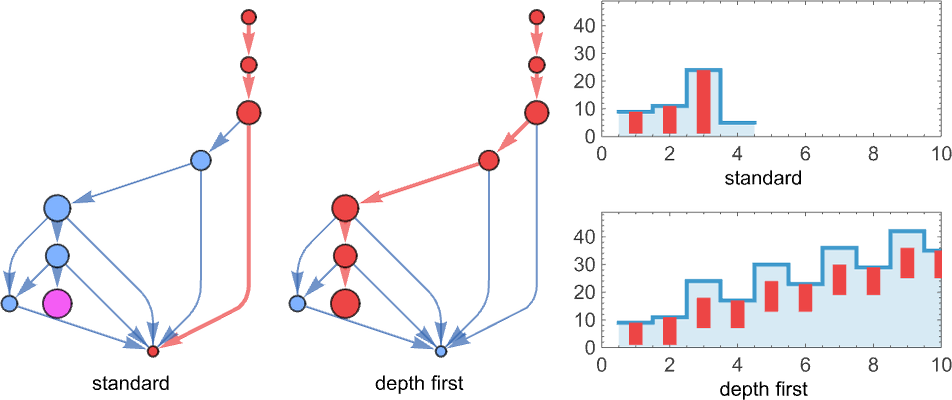
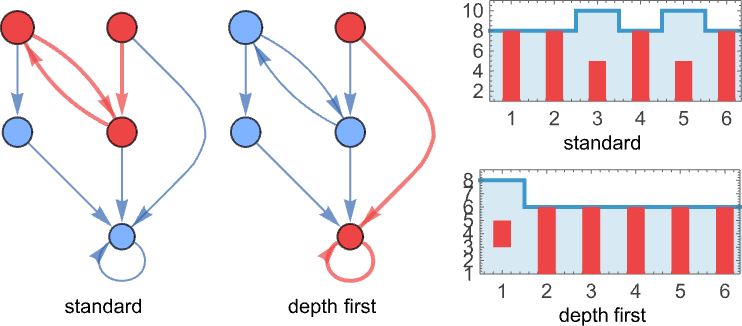
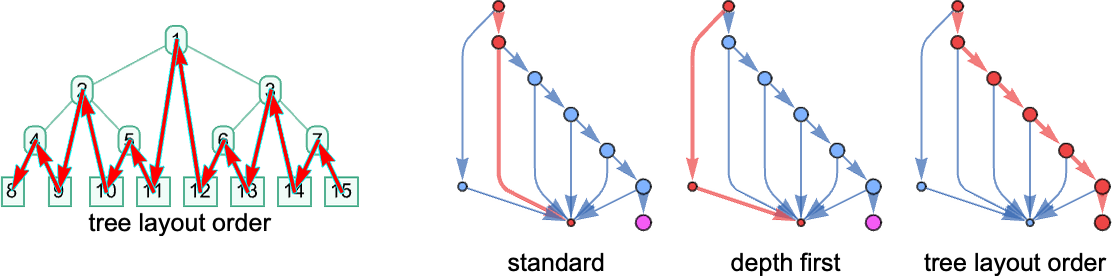
In terms of the structure of the tree, this corresponds to picking the leftmost outermost beta reduction, i.e. the one that in our rendering of the tree is “highest and furthest to the left”:
So what are some other strategies we could use? One way we can specify a strategy is by giving an algorithm that picks one list out of any collection of lists of 0’s and 1’s. (For now we’ll consider only “sequential strategies”, that pick out a single position list—i.e. a single reduction—at a time.) But another way to specify a strategy is to define an ordering on the expression tree, then to say that the beta reduction we’ll do is the one we reach first if we traverse the tree in that order. And so, for example, our leftmost outermost strategy is associated with a breadth-first traversal of the tree. Another evaluation strategy is leftmost innermost, which is associated with a depth-first traversal of the tree, and a purely lexicographic ordering, independent of length, of all tree positions of beta reductions.
In the Wolfram Language, the option TreeTraversalOrder gives detailed parametrizations of possible traversal orders for use in functions like TreeMap—and each of these orders can be used to define an evaluation strategy for lambdas. The standard ReplaceAll (/.) operation applied to expression trees in the Wolfram Language also defines an evaluation strategy—which turns out to be exactly our standard outermost leftmost one. Meanwhile, using standard Wolfram Language evaluation after giving an assignment λ[x_][y_]:=… yields the leftmost innermost evaluation strategy (since at every level the head λ[…] is evaluated before the argument). If the λ had a Hold attribute, however, then we’ll instead get what we can call “applicative” order, in which the arguments are evaluated before the body. And, yes, this whole setup with possible evaluation strategies is effectively identical to what I discussed at some length for combinators a few years ago.
OK, so what happens with different strategies? Here are examples of the evaluation chains generated in various different cases:
Each of these corresponds to following a different path in the multiway graph:
And each, in effect, corresponds to a different way to reach the final result:
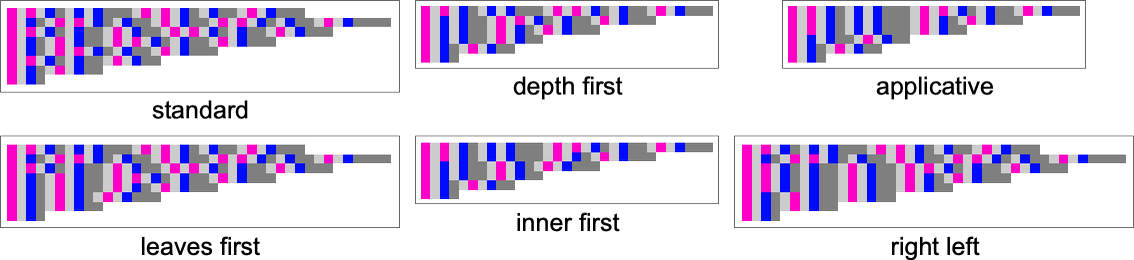
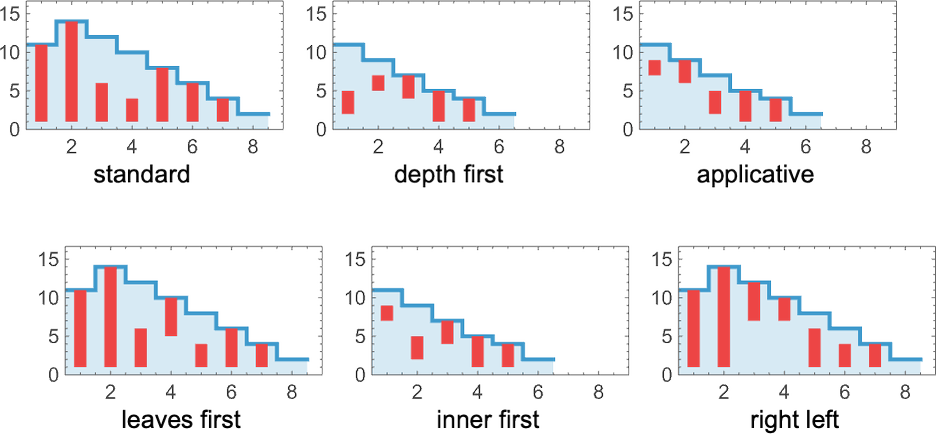
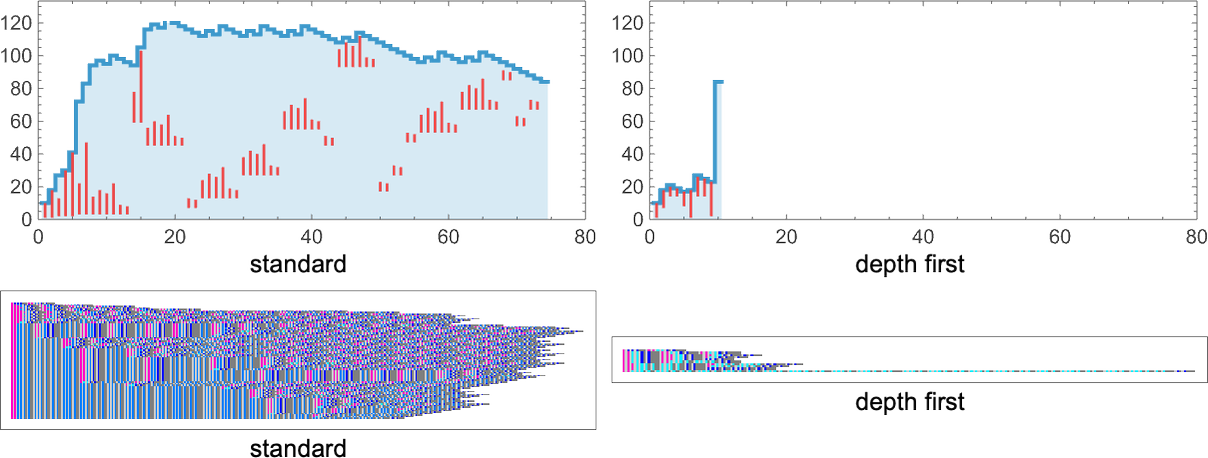
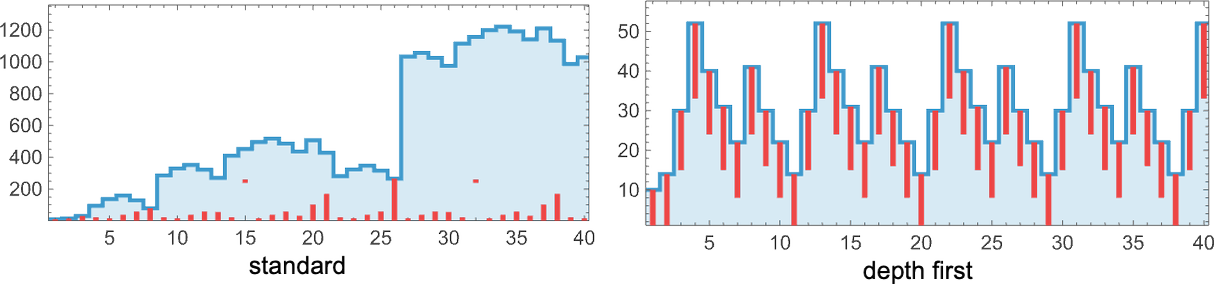
Plotting the sizes of lambdas obtained at each step, we see that different strategies have different profiles—notably in this case with the standard strategy taking more steps to reach the final result than, for example, depth first:
OK, but so what exactly do these strategies mean? In terms of Wolfram Language function TreeTraversalOrder they are (“applicative” involves dependence on whether an element is a λ or a •, and works slightly differently):
In terms of tree positions, these correspond to the following orderings
which correspond to these paths through nodes of a tree:
As we mentioned much earlier, it is a general feature of lambdas that if the evaluation of a particular
lambda terminates, then the result obtained must always be the same—independent of the evaluation
strategy used. In other words, if there are terminating paths in the multiway graph, they must all
converge to the same fixed point. Some paths may be shorter than others, representing the fact that some
evaluation strategies may be more efficient than others. We saw one example of this above, but the
differences can be much more dramatic. For example,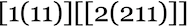 
takes 74 steps to terminate with our
standard evaluation strategy, but only 10 with depth first:
And indeed it’s fairly common to see cases where standard evaluation and depth first produce very different behavior; sometimes one is more efficient, sometimes it’s the other. But despite differences in “how one gets there”, the final fixed-point results are inevitably always the same.
But what happens if only some paths in the multiway graph terminate? That’s not something that happens
with any lambdas up to size 8. But at size 9, for example,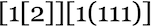 
terminates with standard evaluation
but not with depth first:
And an even simpler example is 
:
In both these cases, standard evaluation leads to termination, but depth-first evaluation does not. And in fact it’s a general result that if termination is ever possible for a particular lambda, then our standard (“leftmost outermost”) evaluation strategy will successfully achieve it.
But what if termination is never possible? Different evaluation strategies can lead to different
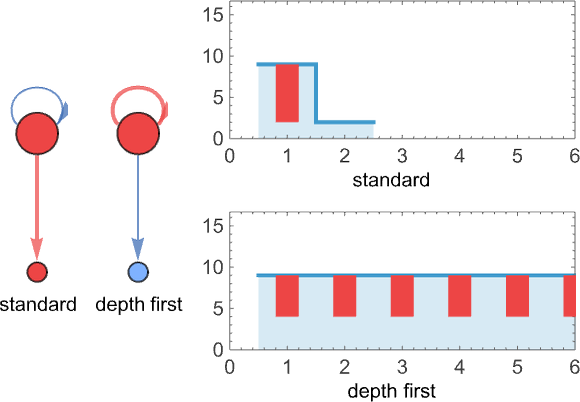
behavior. For example, 
can get stuck in a loop of either
period 2 or period 1:
It’s also possible for one strategy to give lambdas that grow forever, and another to give lambdas that
are (as in this 
case), say, periodic in size—in effect
showing two different ways of not terminating:
But what if one has a whole collection of lambdas? What generically happens? Within every multiway graph there can be a fixed point, some number of loops and some (tree-like) unbounded growth. Every strategy defines a path in the multiway graph—which can potentially lead to any of these possible outcomes. It’s fairly typical to see one type of outcome be much more likely than others—and for it to require some kind of “special tuning” to achieve a different type of outcome.
For this case
almost all evaluation strategies lead to termination—except the particular strategy based on what we might call “tree layout order”:
So what happens if we use a strategy where at each step we just pick between different possible beta reductions at random, with equal probability? Here are some examples for the [1(11)][[2(211)]] lambda we saw above, that takes 74 steps to terminate with our standard evaluation strategy:
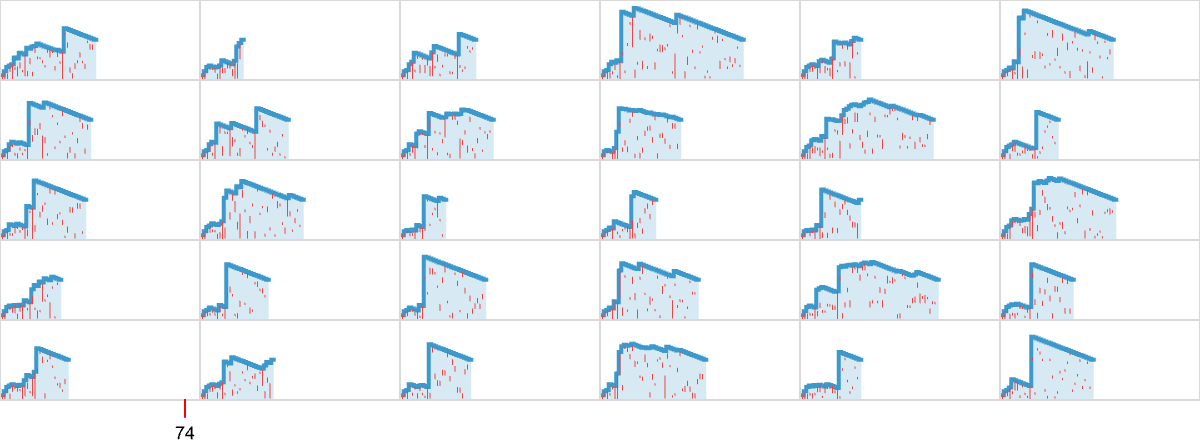
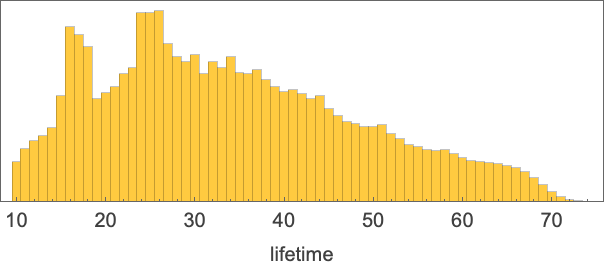
There’s quite a diversity in the shapes of curves generated. But it’s notable that no nonterminating cases are seen—and that termination tends to occur considerably more quickly than with standard evaluation. Indeed, the distribution of termination times only just reaches the value 74 seen in the standard evaluation case:
For lambdas whose evaluation always terminates, we can think of the sequence of sizes of expressions generated in the course of their evaluation as being “pinned at both ends”. When the evaluation doesn’t terminate, the sequences of sizes can be wilder, as in these [11][1(1(1[[3]]))] cases:
The Equivalence of Lambdas
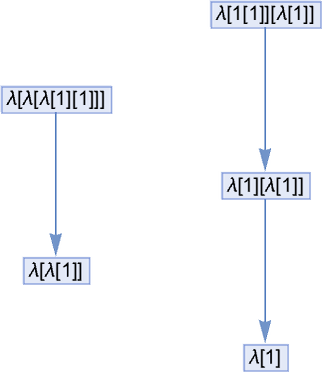
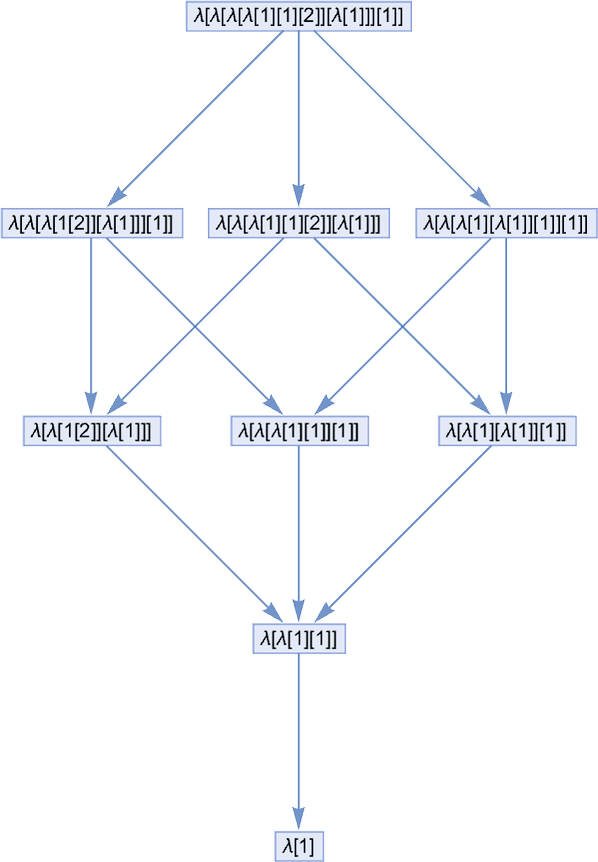
Consider the lambdas:
They each have a different form. But they all evaluate to the same thing: λ[1]. And particularly if we’re thinking about lambdas in a mathematically oriented way this means we can think of all these lambdas as somehow “representing the same thing”, and therefore we can consider them “equivalent”.
Out of all 18 lambdas up to size 4, these three are actually the only ones that are equivalent in this sense. So that means there are 15 “evaluation inequivalent” lambdas up to size 4.
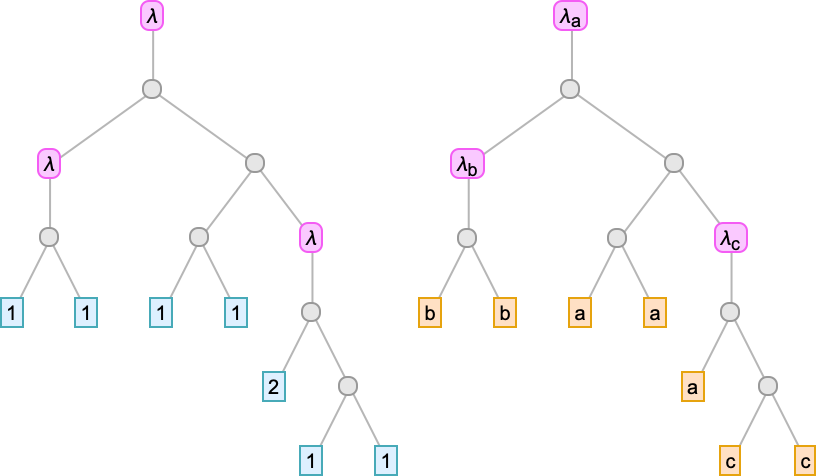
Up to size 5, there are a total of 100 forms of lambdas—which evolve to 68 distinct final results—and there are 4 multi-lambda equivalence classes
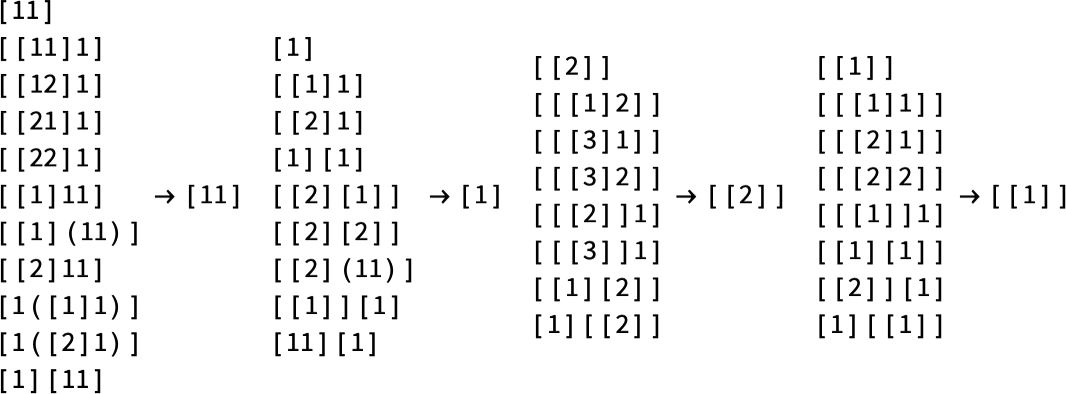
which we can summarize graphically as:
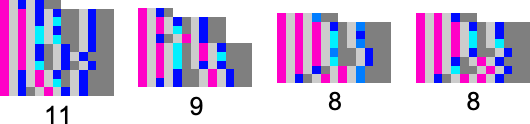
Up to size 6, there are a total of 679 forms of lambdas—which evolve to 392 distinct final states (along with one “looping lambda”)—and there are 16 multi-lambda equivalence classes:
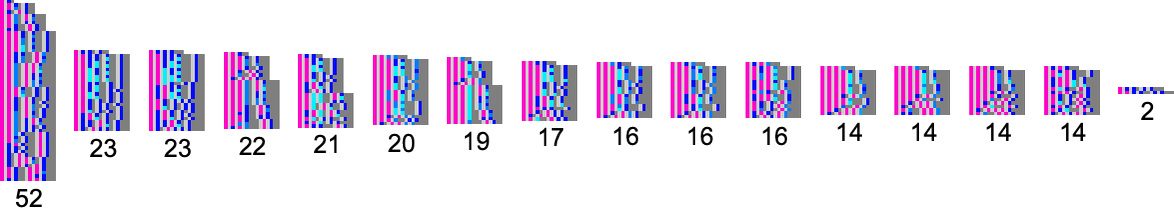
If we look only at lambdas whose evaluation terminates then we have the following:
For large sizes, the ratio conceivably goes more or less exponentially to a fixed limiting value around 1/4.
But this is only for lambdas that terminate. So what can we say about equivalences between lambdas that don’t terminate? Well, it depends what we mean by “equivalence”. One definition might be that two lambdas are equivalent if somewhere in their evolution they generate identical lambda expressions. Or, in other words, there is some overlap in their multiway graphs.
If we look up to size 7, there are 8 lambdas that don’t terminate, and there’s a single—rather simple—correspondence between their multiway systems:
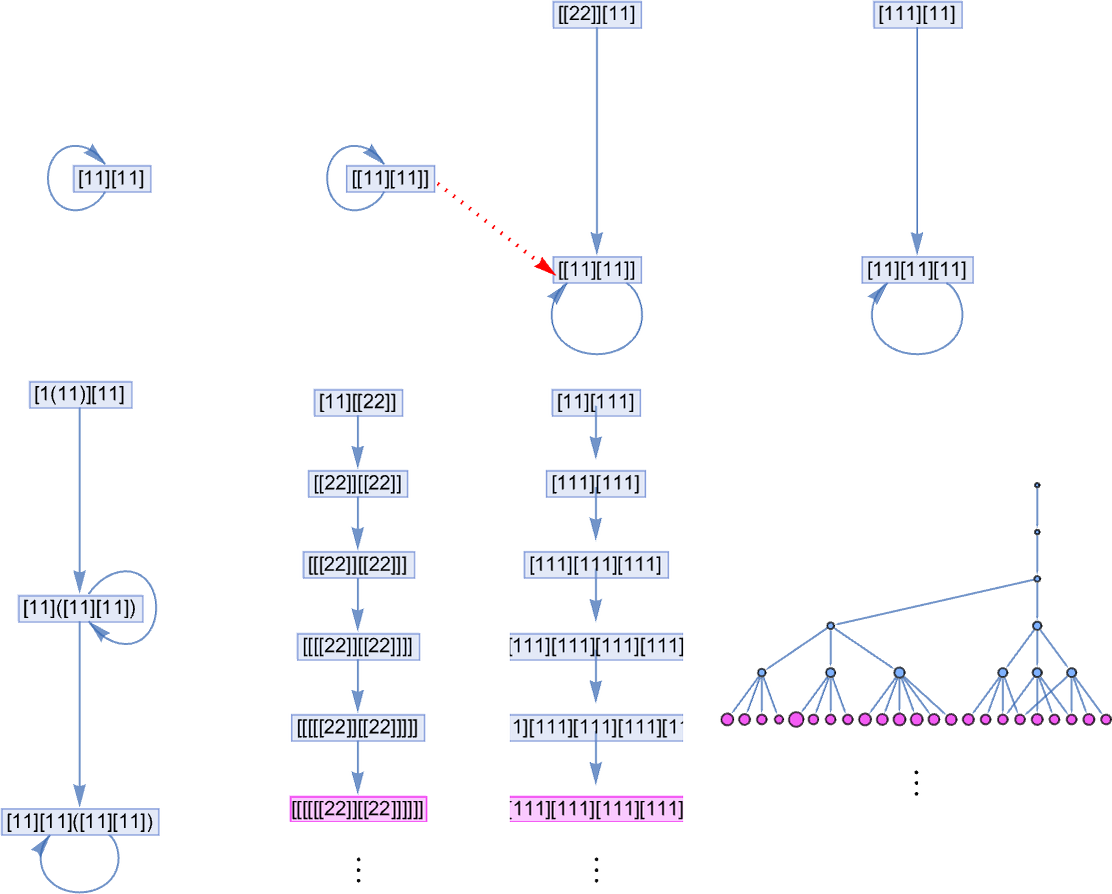
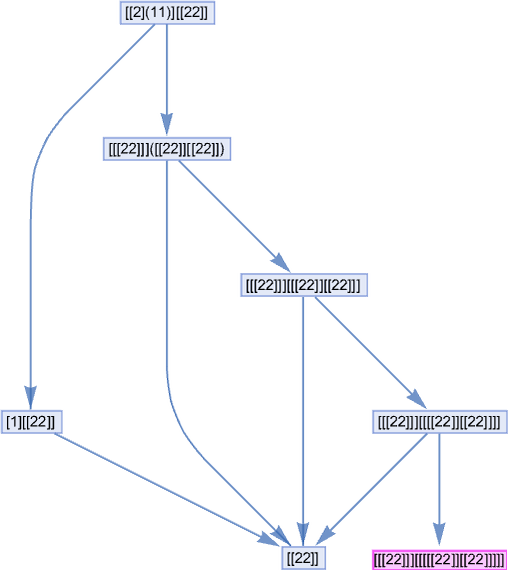
Up to size 8, there are 89 lambdas whose evaluation doesn’t terminate. And among these, there are many correspondences. A simple example is:
More elaborate examples include
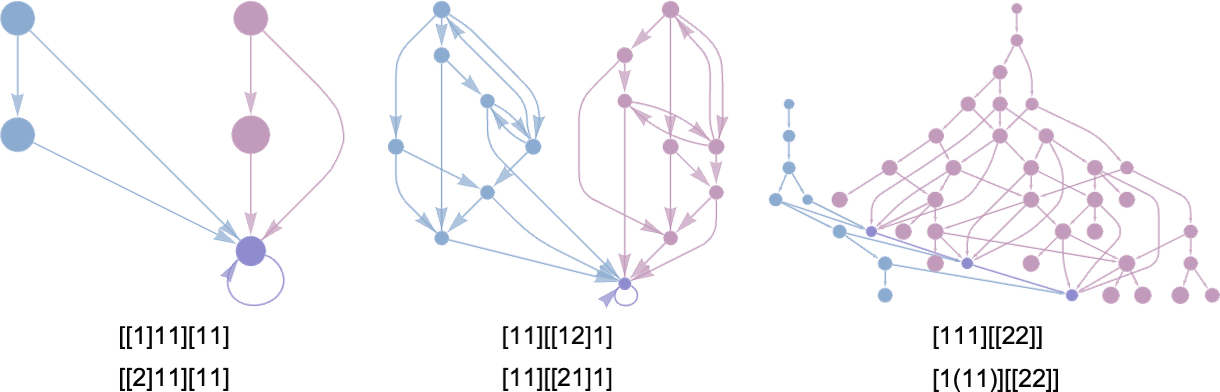
where now we are showing the combined multiway graphs for pairs of lambdas. In the first two cases, the overlap is at a looping lambda; in the third it is at a series of lambda expressions.
If we look at all 89 nonterminating lambdas, this shows which are the 434 overlapping pairs:
There are several subtleties here. First, whether two lambdas are “seen to be equivalent” can depend on the evaluation strategy one’s using. For example, a lambda could terminate for one strategy, but can “miss the fixed point” with another strategy that fails to terminate.
In addition, even if the multiway graphs for two lambdas overlap, there’s no guarantee that that overlap will be “found” with any given evaluation strategy.
And, finally, as so often, there’s an issue of undecidability. Even if a lambda is going to terminate, it can take an arbitrarily long time to do so. And, worse, if one progressively generates the multiway graphs for two lambdas, it can be arbitrarily difficult to see if they overlap. Determining a single evaluation path for a lambda can be computationally irreducible; determining these kinds of overlaps can be multicomputationally irreducible.
Causality for Lambdas
We can think of every beta reduction in the evaluation of a lambda as an “event” in which certain input is transformed to certain output. If the input to one event V relies on output from another event U, then we can say that V is causally dependent on U. Or, in other words, the event V can only happen if U happened first.
If we consider a lambda evaluation that involves a chain of many beta reductions, we can then imagine building up a whole “causal graph” of dependencies between beta reduction events.
As a simple example, consider this evaluation chain, where we’ve explicitly shown the beta reduction events, and (for clarity in this simple case) we’ve also avoided renaming the variables that appear:
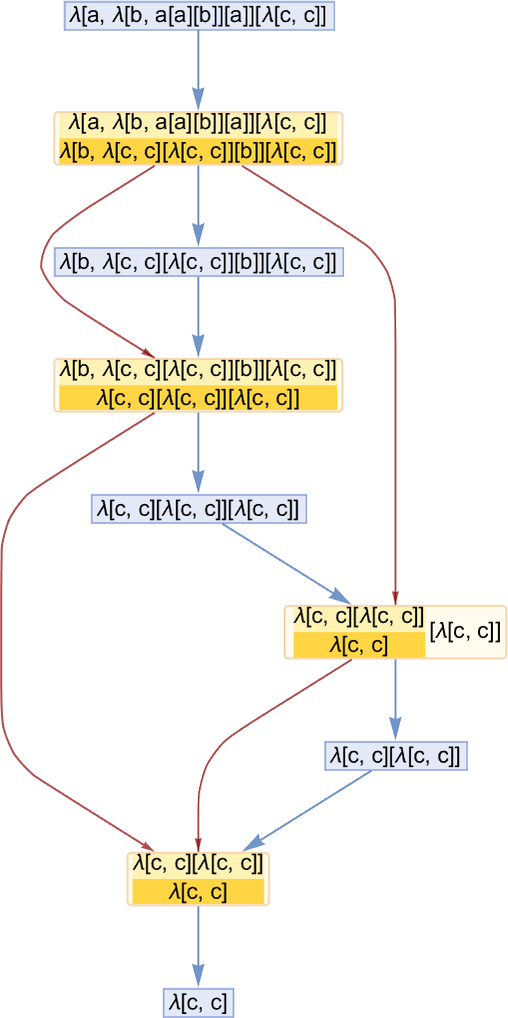
The blue edges here show how one lambda transforms to another—as a result of an event. The dark red edges show the causal relations between events; each of them can be thought of as being associated with a subexpression that is the “carrier of causality” from one event to another.
Keeping only events and causal edges, the causal graph for this evolution is then:
If we follow a sequence of causal edges we get a “timelike” chain of events that must occur in order. But “transverse” to that we can have (in the language of posets) an “antichain” consisting of what we can think of as “spacelike separated” events that can occur in parallel. In this case the first event (i.e. the first beta reduction) leads to the expression
in which there are two reductions that can be done: for λ[b,…] and for the first λ[c,…]. But these reductions are completely independent of each other; they can be thought of as “spacelike separated”. In our standard evaluation scheme, these events occur in a definite order. But what the causal graph shows is that the result we get doesn’t require that order—and indeed allows these events to occur “in parallel”.
Many lambdas don’t allow parallelization in their evaluation, so have simple, linear causal graphs:
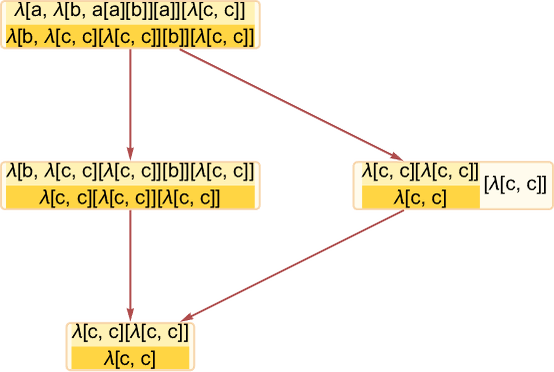
It’s common to have simple branching in the causal graph—associated with pieces of the λ expression that are completely separated as far as beta reduction is concerned, and can be evaluated separately:
One tricky issue that arises in constructing causal graphs for lambdas is figuring out exactly what is really dependent on what. In this case it might seem that the two events are independent, since the first one involves λ[a,…] while the second one involves λ[b,...]. But the second one can’t happen until the λ[b, ...] is “activated” by the reduction of λ[a, ...] in the first event—with the result that second event must be considered causally dependent on the first, as recorded in the causal graph:
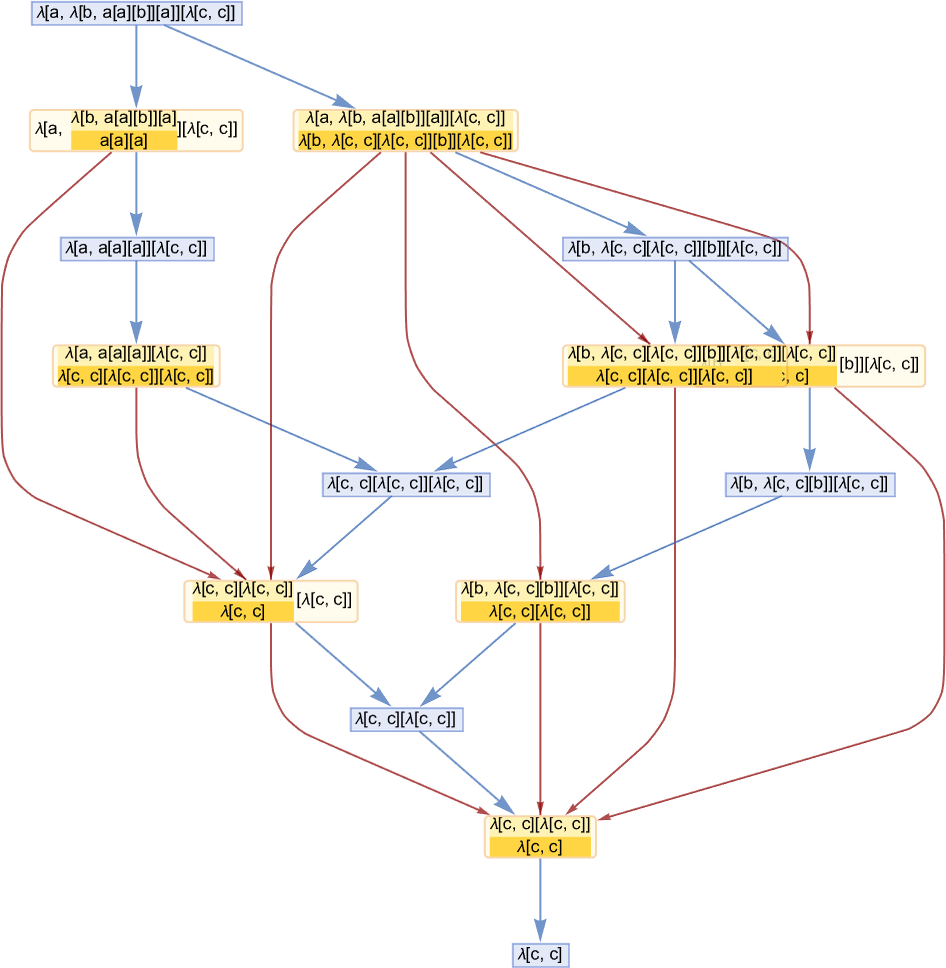
While many lambdas have simple, linear or branched causal graphs, plenty have more complicated structures. Here are some examples for lambdas that terminate:
Lambdas that don’t terminate have infinite causal graphs:
But what’s notable here is that even when the evolution—as visualized in terms of the sequence of sizes of lambdas—isn’t simple, the causal graph is still usually quite simple and repetitive. And, yes, in some cases seeing this may well be tantamount to a proof that the evolution of the lambda won’t terminate. But a cautionary point is that even for lambdas that do terminate, we saw above that their causal graphs can still look essentially repetitive—right up to when they terminate.
Multiway Causal Graphs
The causal graphs we showed in the previous section are all based on analyzing causal dependencies in specific lambda evaluation chains, generated with our standard (leftmost outermost) evaluation scheme. But—just like in our Physics Project—it’s also possible to generate multiway causal graphs, in which we show causal connections between all states in the multiway graph representing all possible evaluation sequences.
Here’s the multiway version of the first causal graph we showed above:
Some causal graphs remain linear even in the multiway case, but others split into many paths:
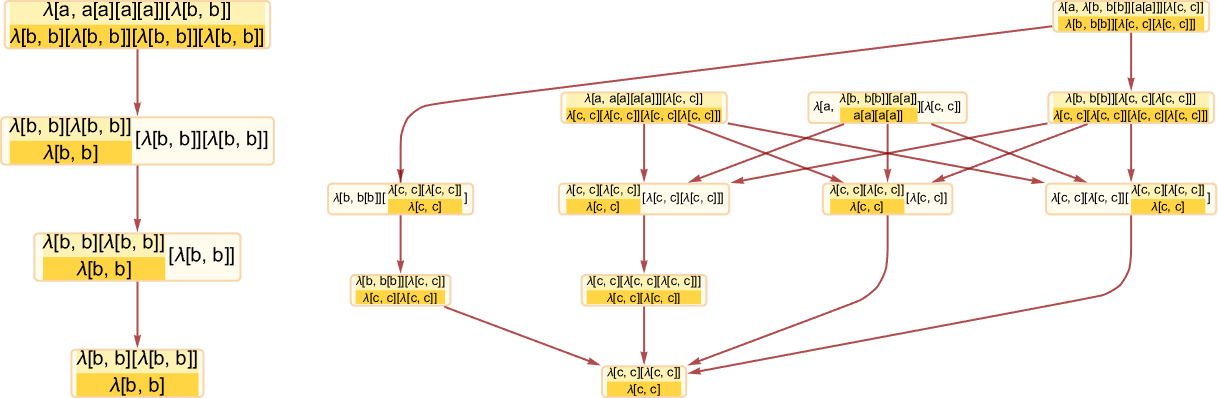
It’s fairly typical for multiway causal graphs to be considerably more complicated than ordinary causal graphs. So, for example, while the ordinary causal graph for [1(11)][[212]] is
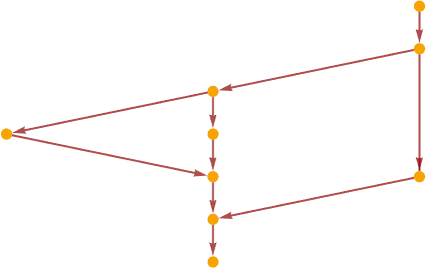
the multiway version is
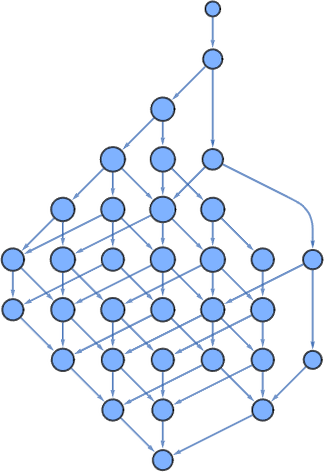
while the multiway graph for states is:
So, yes, it’s possible to make multiway causal graphs for lambdas. But what do they mean? It’s a somewhat complicated story. But I won’t go into it here—because it’s basically the same as the story for combinators, which I discussed several years ago. Though lambdas don’t allow one to set up the kind of shared-subexpression DAGs we considered for combinators; the variables (or de Bruijn indices) in lambdas effectively lead to long-range correlations that prevent the kind of modular treelike approach we used for combinators.
The Case of Linear Lambdas
We’ve seen that in general lambdas can do very complicated things. But there’s a particular class of lambdas—the “linear lambdas”—that behave in much simpler ways, allowing them to be rather completely analyzed. A linear lambda is a lambda in which every variable appears only once in the body of the lambda. So this means that λ[a, a] is a linear lambda, but λ[a, a[a]] is not.
The first few linear lambdas are therefore
or in de Bruijn index form:
Linear lambdas have the important property that under beta reduction they can never increase in size. (Without multiple appearances of one variable, beta reduction just removes subexpressions, and can never lead to the replication of a subexpression.) Indeed, at every step in the evaluation of a linear lambda, all that can ever happen is that at most one λ is removed:
Since linear lambdas always have one variable for each λ, their size is always an even number.
The number of linear lambdas is
small compared to the total number of lambdas of a given size:
(Asymptotically, the number of linear lambdas of size 2m grows like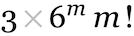 
.)
Here are the Tromp diagrams for the size-6 linear lambdas:
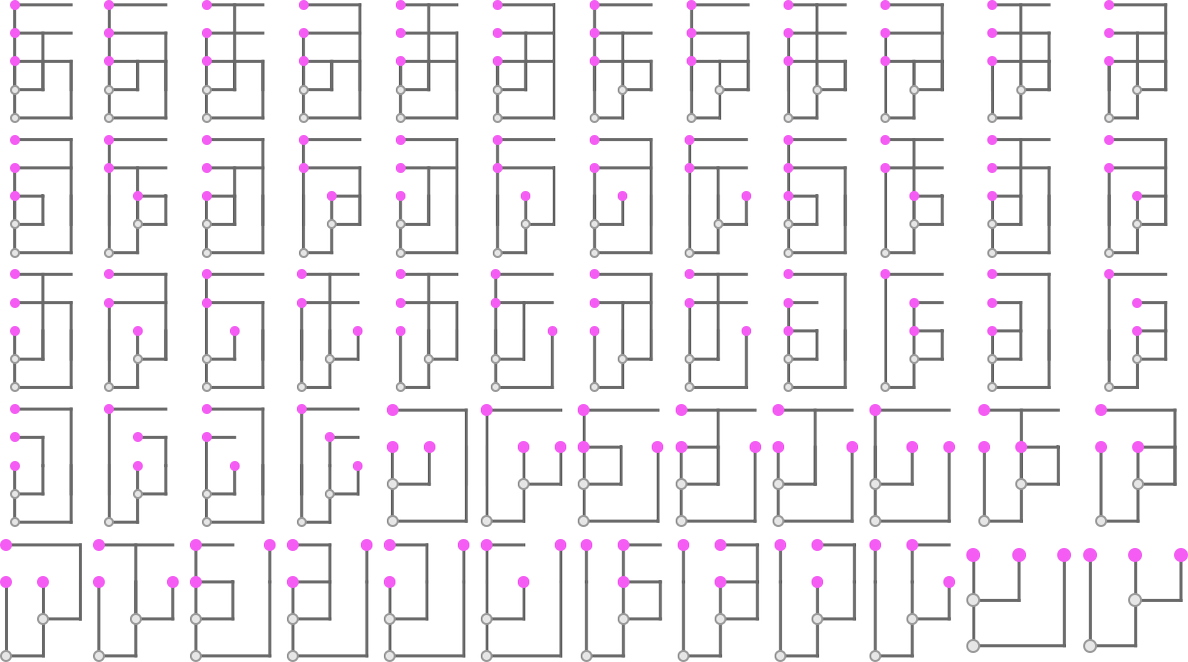
Evaluation always terminates for a linear lambda; the number of steps it takes is independent of the evaluation scheme, and has a maximum equal to the number of λ’s; the distribution for size-6 linear lambdas is:
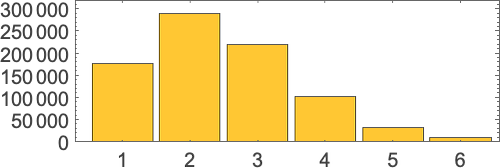
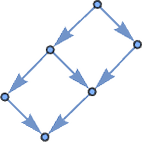
The multiway graphs for linear lambdas are rather simple. Since every λ is independent of every other, it never matters in what order they are reduced, and the multiway graph consists of a collection of diamonds, as in for example:
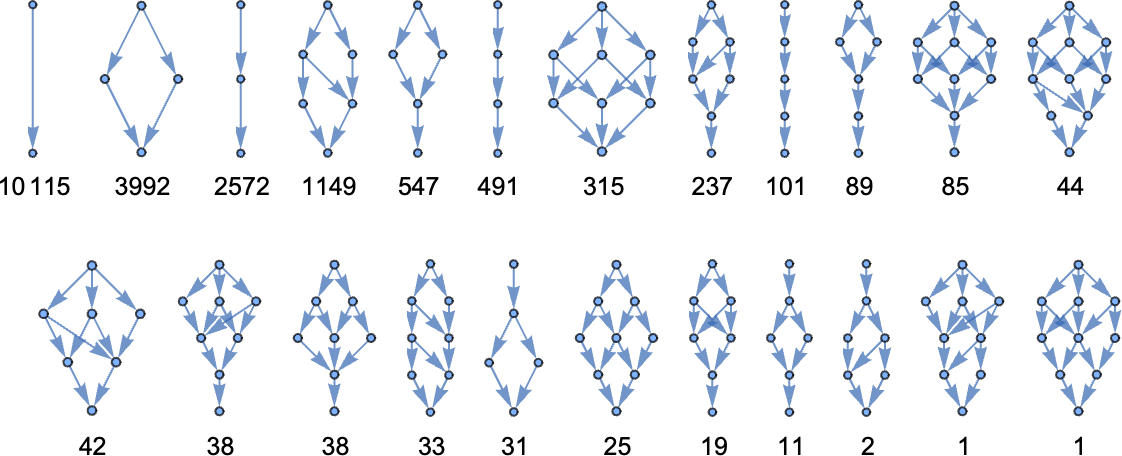
For size 6 the possible multiway graphs (with their multiplicities) are:
For size 8 it’s
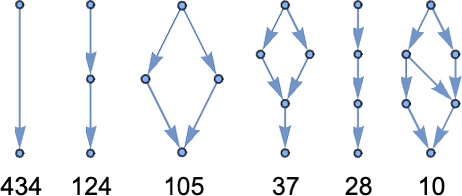
where the last graph can be drawn in a more obviously symmetrical way as:
And for size 10 it’s:
In addition to looking at linear lambdas, we can also look at affine lambdas, which are defined to allow zero as well as one instance of each variable. The affine lambdas behave in a very similar way to the linear lambdas, except that now there are some “degenerate diamond structures” in the multiway graph, as in:
Lambdas versus Combinators
So now that we’ve explored all this ruliology for lambdas, how does it compare to what I found several years ago for combinators? Many of the core phenomena are certainly very much the same. And indeed it’s easy to convert between lambdas and combinators—though a lambda of one size may correspond to a combinator of a very different size.
For example, the size-4 lambdas have these equivalent combinators
while the size 3 combinators have these equivalent lambdas:
Not surprisingly, the (LeafCount) size of lambdas tends to be slightly smaller for the equivalent combinators, because the presence of de Bruijn indices means lambdas effectively have a larger “alphabet” to work with.
But in the end, lambdas and combinators can “do all the same things”, as in these cases:
The Principle of Computational Equivalence implies that at a fundamental level the ruliology of systems whose behavior is not obviously simple will be at least at some level the same.
But lambdas have definitely given us some unique challenges. First, there is the matter of variables and the nonlocality they imply. It’s not like in a cellular automaton or a Turing machine where in a sense every update happens locally. Nor is it even like in combinators, where things are local at least on a tree—or hypergraph rewriting systems where things are local on a hypergraph. Lambdas are both hierarchical and nonlocal. Lambda expressions have a tree structure, but variables knit pieces of this tree together in arbitrarily complex ways. And beta reduction can in effect pull on arbitrarily long threads.
All of this then gets entangled with another issue: lambdas routinely can get very big. And even that wouldn’t be such a problem if it wasn’t for the fact that there’s no obvious way to compress what the lambdas do. With the result that even though the Wolfram Language gives one a very efficient way to deal with symbolic structures, the things I’ve done here have often challenged my computational resources.
Still, in the end, we’ve managed to do at least the basics in exploring the ruliology of lambdas, and have seen that yet another corner of the computational universe is full of remarkable and surprising phenomena. I first wondered what lambdas might be “like in the wild” back at the beginning of the 1980s. And I’m pleased that finally now—so many years later—I’ve finally been able to get a sense of the world of lambdas and both the uniqueness and the sameness of their ruliology.
Bibliographic Note
An immense amount has been written about lambdas over the past 90 years, though in most cases its focus has been formal and theoretical, not empirical and ruliological. When I wrote about combinators in 2020 I did the scholarship to compile a very extensive bibliography of the (considerably smaller) literature about combinators. For lambdas I have not attempted a similar exercise. But given the overlap—and equivalence—between combinators and lambdas, much of my combinator bibliography also applies to lambdas.
Thanks
Thanks to Wolfram Institute Fellows Nik Murzin and Willem Nielsen for extensive help. Also thanks to several others affiliated with the Wolfram Institute, especially Richard Assar and Joseph Stocke. In addition, for specific input about what I describe here I thank Alex Archerman, Utkarsh Bajaj, Max Niederman, Matthew Szudzik, and Victor Taelin. Over the years I’ve interacted about lambdas with many people, including Henk Barendregt, Greg Chaitin, Austin Jiang, Jan Willem Klop, Roman Maeder, Dana Scott and John Tromp. And at a practical level I’ve had innumerable discussions since the late 1970s about the Function function in Wolfram Language and Mathematica, as well as its predecessor in SMP.
