Institute Output
Kolmogorov Complexity vs. Computational Irreducibility: Understanding the Distinction
James K. Wiles
Kolmogorov complexity and computational irreducibility describe two kinds of limits on simplification, but they apply in different ways. Kolmogorov complexity measures the shortest possible description of an object, such as a string. Computational irreducibility refers to processes that cannot be predicted or accelerated. This paper introduces each concept, explains their theoretical distinction, and illustrates the difference using simple examples.
Computational Metaphysics: A Survey of the Ruliad, Observer Theory and Emerging Frameworks
James K. Wiles
A concise survey of how recent computational models, such as the ruliad and observer theory, are transforming metaphysical questions into formal, testable frameworks.
On the Nature of Time
Stephen Wolfram
Time is a central feature of human experience. But what actually is it? In traditional scientific accounts it’s often represented as some kind of coordinate much like space (though a coordinate that for some reason is always systematically increasing for us). But while this may be a useful mathematical description, it’s not telling us anything about what time in a sense “intrinsically is”.
On the Concept of Motion
Stephen Wolfram
It seems like the kind of question that might have been hotly debated by ancient philosophers, but would have been settled long ago: how is it that things can move? And indeed with the view of physical space that’s been almost universally adopted for the past two thousand years it’s basically a non-question. As crystallized by the likes of Euclid it’s been assumed that space is ultimately just a kind of “geometrical background” into which any physical thing can be put—and then moved around.
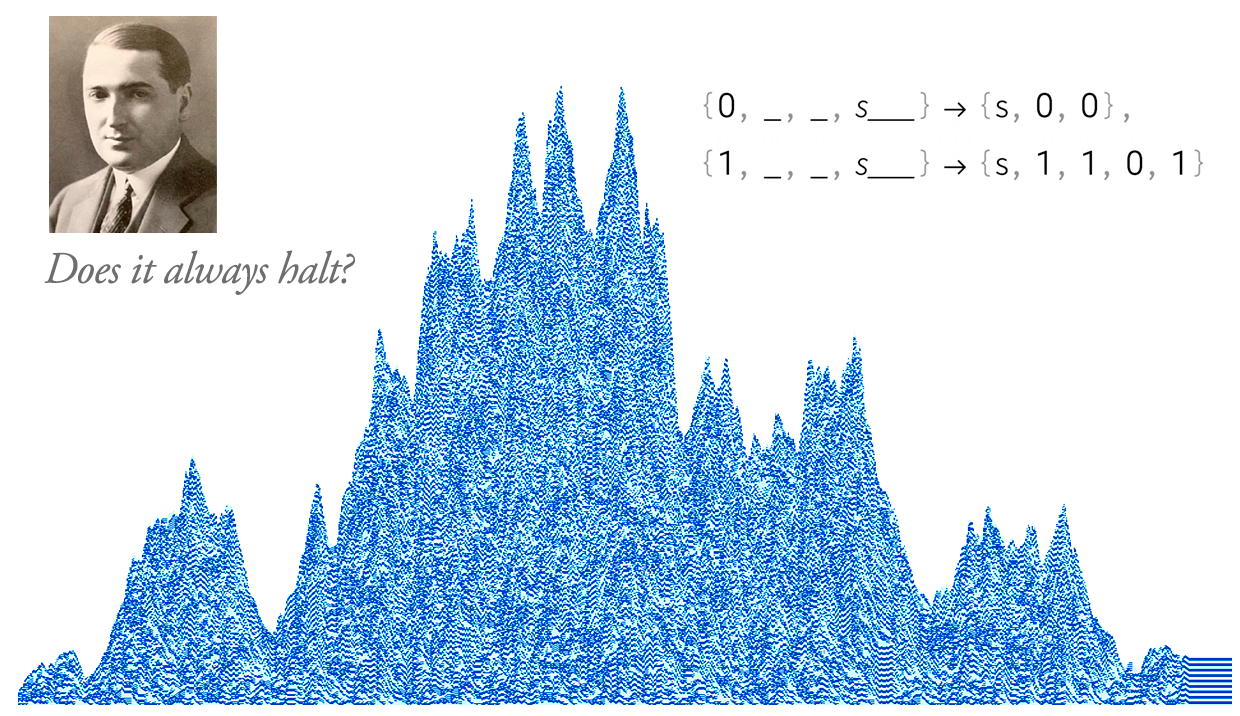
After 100 Years, Can We Finally Crack Post’s Problem of Tag? A Story of Computational Irreducibility, and More
Stephen Wolfram
For Post, the failure to crack his system derailed his whole intellectual worldview. For me now, the failure to crack Post’s system in a sense just bolsters my worldview—providing yet more indication of the strength and ubiquity of computational irreducibility and the Principle of Computational Equivalence.