Institute Output

A Cosine Rule-Based Discrete Sectional Curvature for Graphs
Xerxes D. Arsiwalla, J.F. Du Plessis
How does one generalize differential geometric constructs such as curvature of a manifold to the discrete world of graphs and other combinatorial structures? This problem carries significant importance for analyzing models of discrete spacetime in quantum gravity; inferring network geometry in network science; and manifold learning in data science. The key contribution of this paper is to introduce and validate a new estimator of discrete sectional curvature for random graphs with low metric-distortion.

On the Concept of Motion
Stephen Wolfram
It seems like the kind of question that might have been hotly debated by ancient philosophers, but would have been settled long ago: how is it that things can move? And indeed with the view of physical space that’s been almost universally adopted for the past two thousand years it’s basically a non-question. As crystallized by the likes of Euclid it’s been assumed that space is ultimately just a kind of “geometrical background” into which any physical thing can be put—and then moved around.
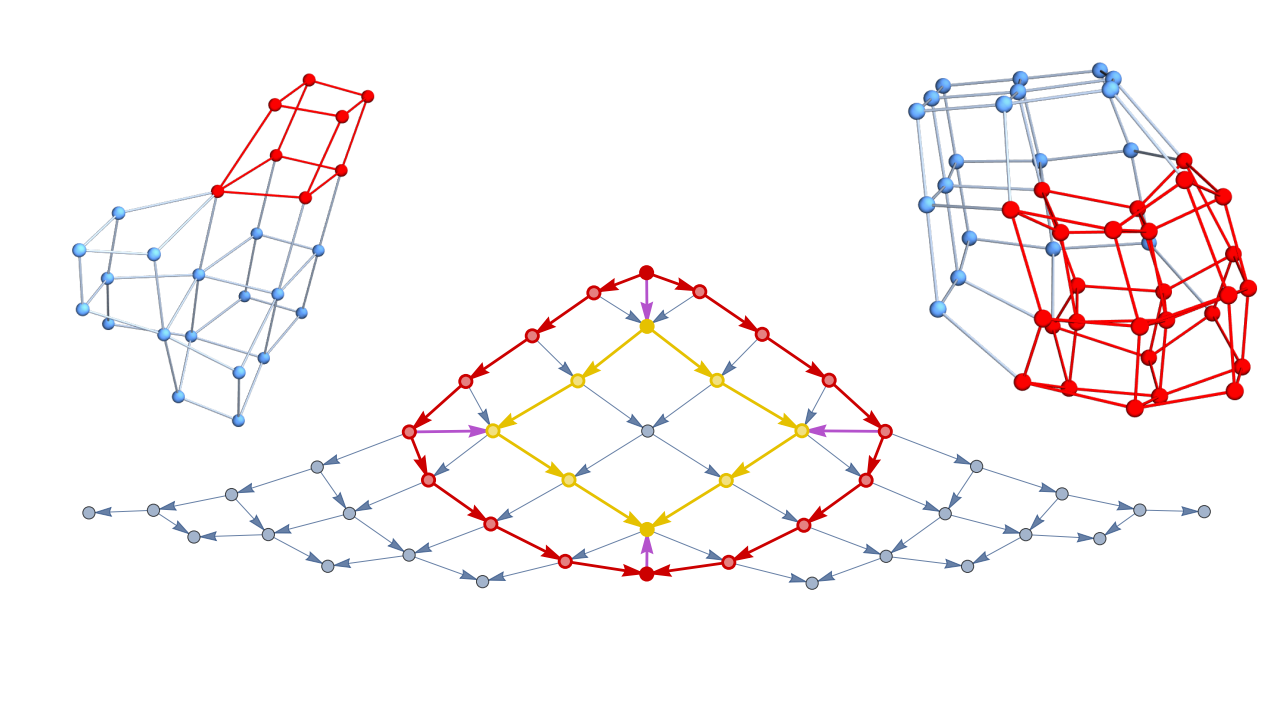
Pregeometric Spaces from Wolfram Model Rewriting Systems as Homotopy Types
Xerxes D. Arsiwalla, Jonathan Gorard
The study explores how spatial structures in physics can emerge from pregeometric combinatorial models governed by computational rules, using higher category theory and homotopy types.
