Institute Output

Quantum Gravity and Computation: Information, Pregeometry, and Digital Physics
Dean Rickles, Xerxes D. Arsiwalla, Hatem Elshatlawy
This volume argues that concepts from the theory of computation—including information theory, formal languages, and discrete structures—might provide novel paths towards a solution to the problem of quantum gravity. By combining elements of physics with computer science and mathematics, the volume proposes to transform the foundations of spacetime physics and bring it into the digital age.

A Cosine Rule-Based Discrete Sectional Curvature for Graphs
Xerxes D. Arsiwalla, J.F. Du Plessis
How does one generalize differential geometric constructs such as curvature of a manifold to the discrete world of graphs and other combinatorial structures? This problem carries significant importance for analyzing models of discrete spacetime in quantum gravity; inferring network geometry in network science; and manifold learning in data science. The key contribution of this paper is to introduce and validate a new estimator of discrete sectional curvature for random graphs with low metric-distortion.

Heaps of Fish: arrays, generalized associativity and heapoids
Carlos Zapata-Carratala, Xerxes D. Arsiwalla, Taliesin Beynon
In this paper we investigate a ternary generalization of associativity by defining a diagrammatic calculus of hypergraphs that extends the usual notions of tensor networks, categories and relational algebras. In doing so we rediscover the ternary structures known as heaps and are able to give a more comprehensive treatment of their mergence in the context of dagger categories and their generalizations.
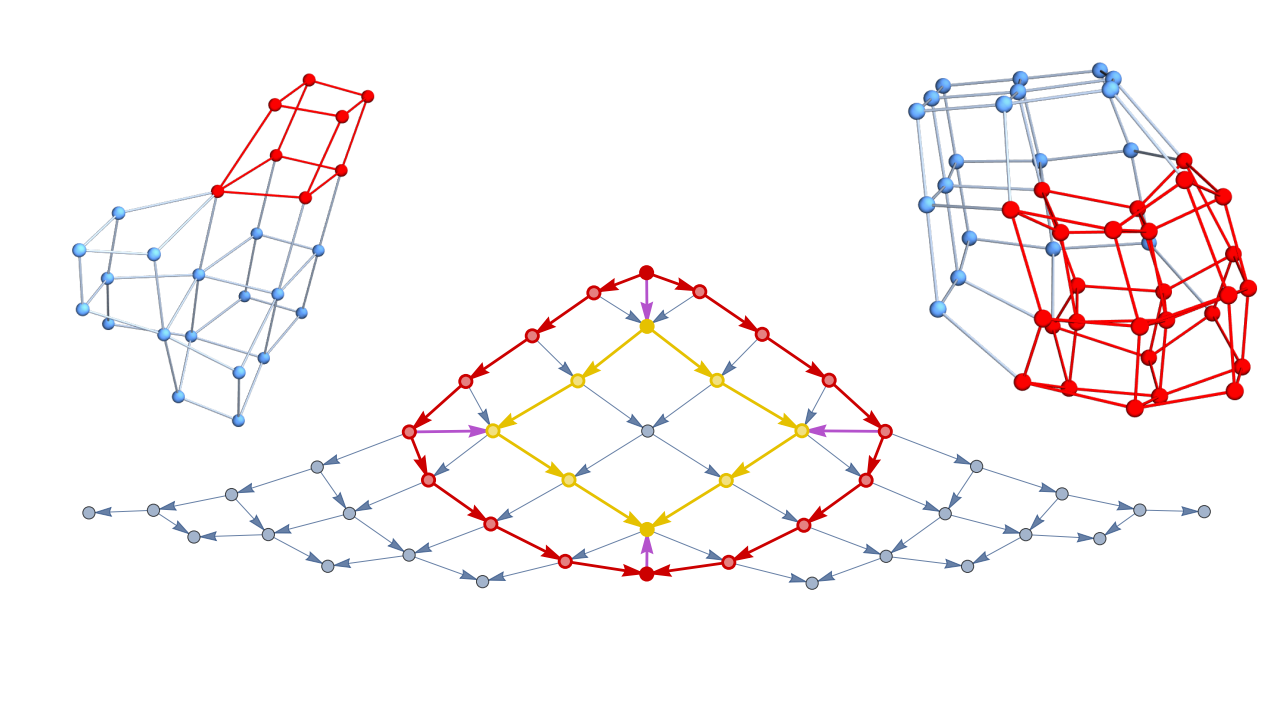
Pregeometric Spaces from Wolfram Model Rewriting Systems as Homotopy Types
Xerxes D. Arsiwalla, Jonathan Gorard
The study explores how spatial structures in physics can emerge from pregeometric combinatorial models governed by computational rules, using higher category theory and homotopy types.
