Institute Output
Hypergraph rewriting and Causal structure of $\lambda$-calculus
Utkarsh Bajaj
Hypergraph rewriting is studied through categorical frameworks to establish foundational concepts of events and causality in graph rewriting systems. Novel concepts are introduced within double-pushout rewriting in adhesive categories. An algorithm is constructed to determine causal relations between events during λ-calculus evaluation, with extensions developed for arbitrary λ-expressions.
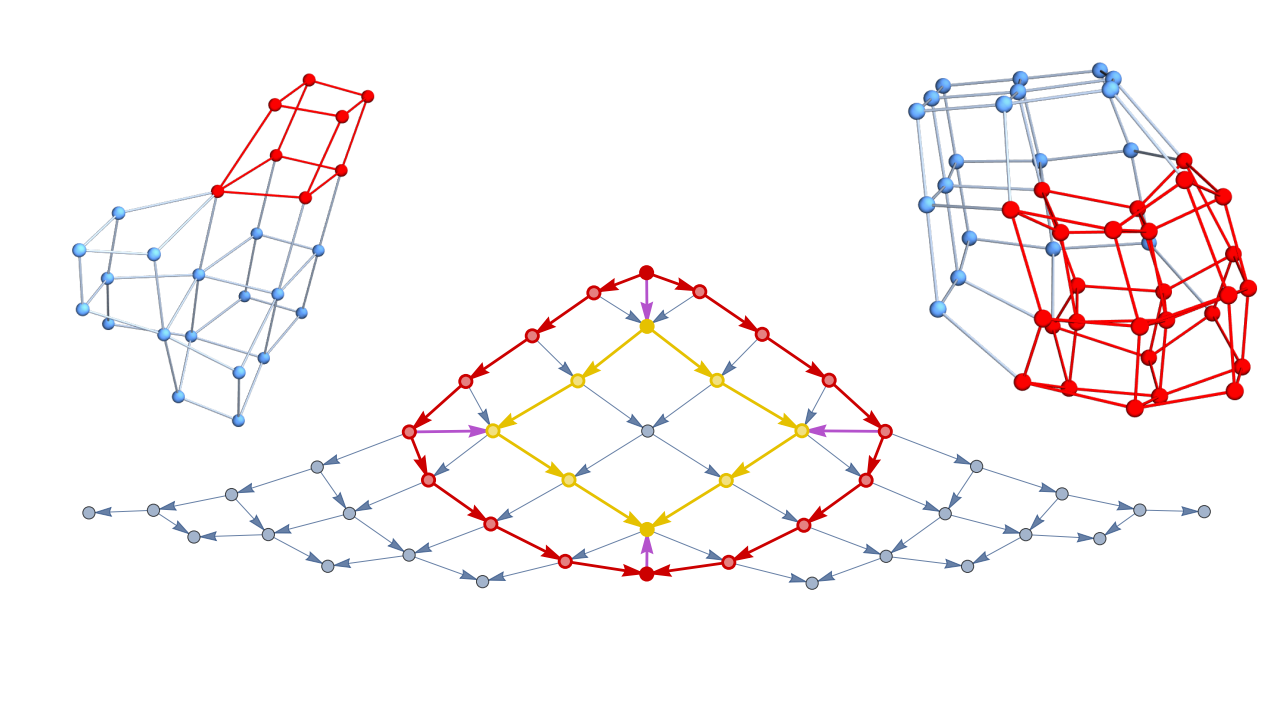
Pregeometric Spaces from Wolfram Model Rewriting Systems as Homotopy Types
Xerxes D. Arsiwalla, Jonathan Gorard
The study explores how spatial structures in physics can emerge from pregeometric combinatorial models governed by computational rules, using higher category theory and homotopy types.