Institute Output
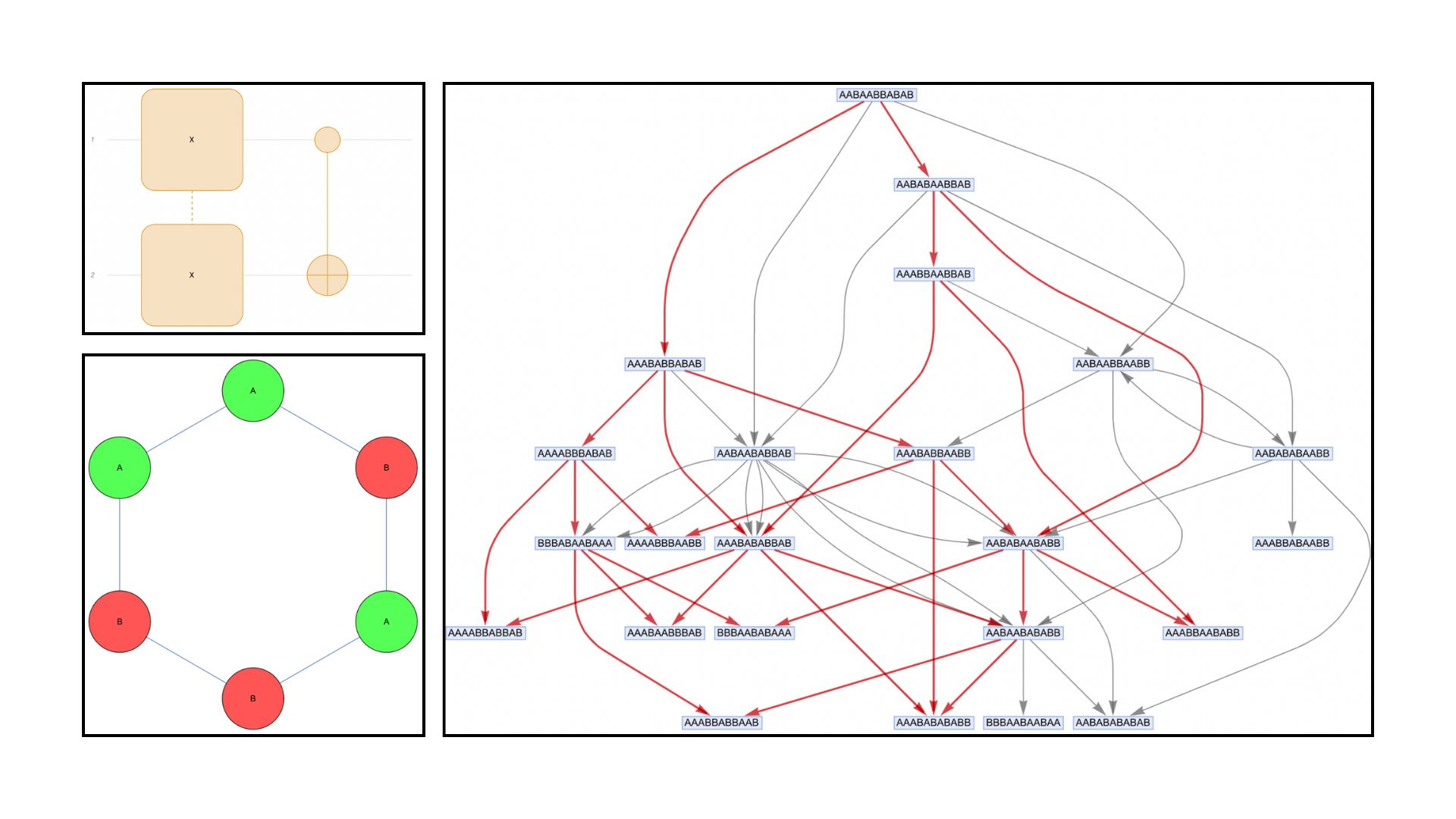
Quantum Operators From Wolfram Model Multiway Systems
Furkan Semih Dündar, Xerxes D. Arsiwalla, Hatem Elshatlawy
Using Wolfram Model multiway rewriting systems we have found that by using multiway systems one can construct representations of quantum circuits, showing that one can encode the Hadamard gate, the π/8 gate and the CNOT using multiway rewriting systems. This suggests the possibility of universal quantum computation using multiway rewriting.
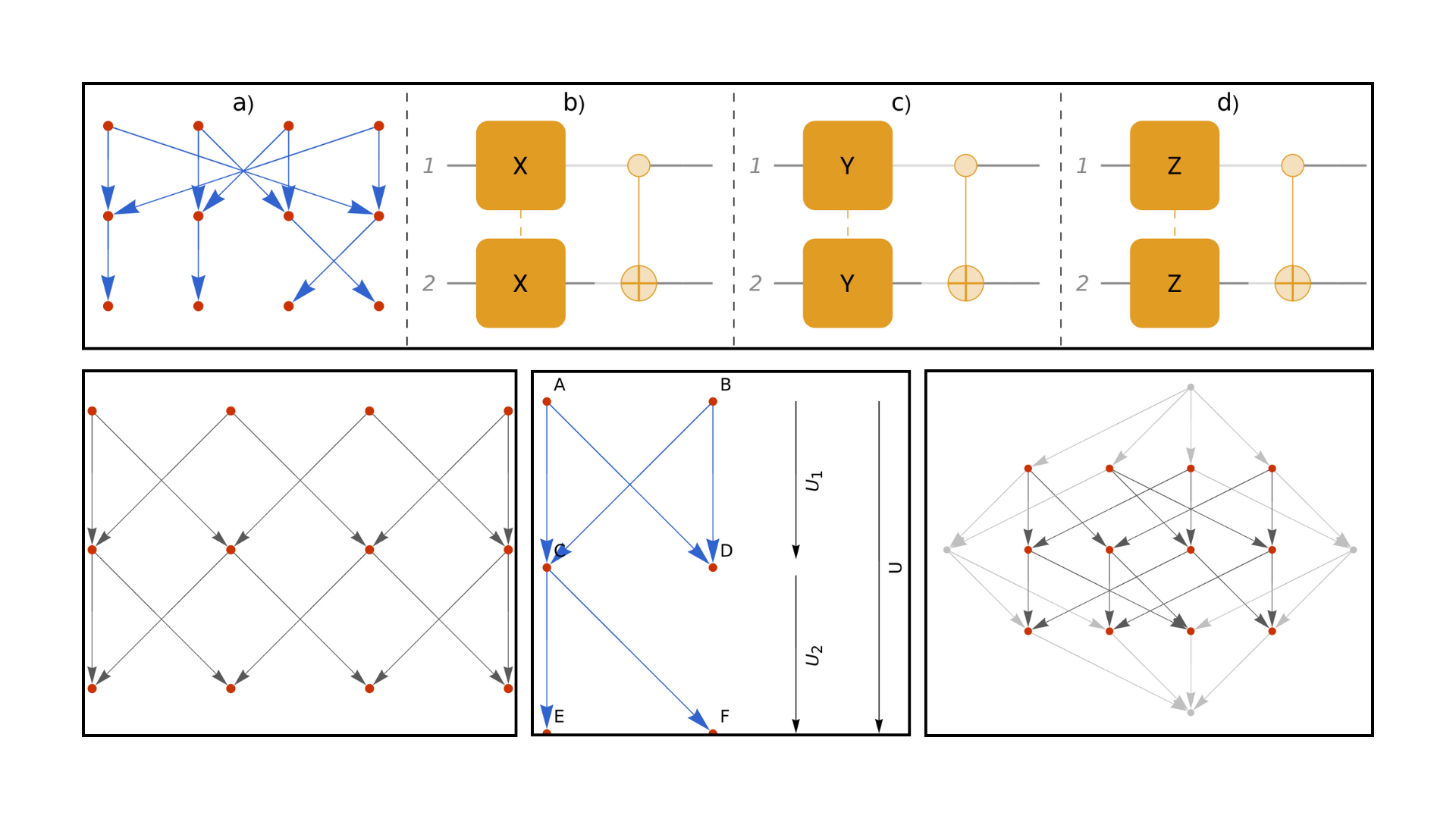
Quantum Gates from Wolfram Model Multiway Rewriting Systems
Furkan Semih Dündar, Xerxes D. Arsiwalla, Hatem Elshatlawy
We show how representations of finite-dimensional quantum operators can be constructed using nondeterministic rewriting systems. In particular, we investigate Wolfram model multiway rewriting systems based on string substitutions.

Quantum Gravity and Computation: Information, Pregeometry, and Digital Physics
Dean Rickles, Xerxes D. Arsiwalla, Hatem Elshatlawy
This volume argues that concepts from the theory of computation—including information theory, formal languages, and discrete structures—might provide novel paths towards a solution to the problem of quantum gravity. By combining elements of physics with computer science and mathematics, the volume proposes to transform the foundations of spacetime physics and bring it into the digital age.

Quantum Potato Chips
Nikolay Murzin, Bruno Tenorio, Sebastian Rodriguez, John McNally, Mohammad Bahrami
This study maps qubit states under symmetric informationally-complete measurements to a tetrahedron in 3D space, identifying a "quantum potato chip" region where quantum states reduce to classical binary variables. States in this special region can be fully reconstructed using only two projective measurements, unlike states elsewhere in the quantum state space.

On the operator origins of classical and quantum wave functions
Xerxes D. Arsiwalla, David Chester, Louis H. Kauffman
We investigate operator algebraic origins of the classical Koopman–von Neumann wave function $\psi_{KvN}$ as well as the quantum-mechanical one $\psi_{QM}$. In particular $\psi_{KvN}$, and $\psi_{QM}$ are both consequences of this pre-quantum formalism. What this suggests is that neither the Schrödinger equation nor the quantum wave function are fundamental structures.

Some Quantum Mechanical Properties of theWolfram Model
Jonathan Gorard
By exploring hypergraph rules that deliberately break causal invariance, we show that the Wolfram Model’s multiway evolution functions like a quantum superposition whose geometry converges to projective Hilbert space. By proving that observers can “collapse” these histories via Knuth–Bendix completion—and deriving multiway analogues of Einstein’s equations, the path integral and the Schrödinger equation—we unify discrete spacetime, quantum mechanics and relativity within one framework.
