Institute Output
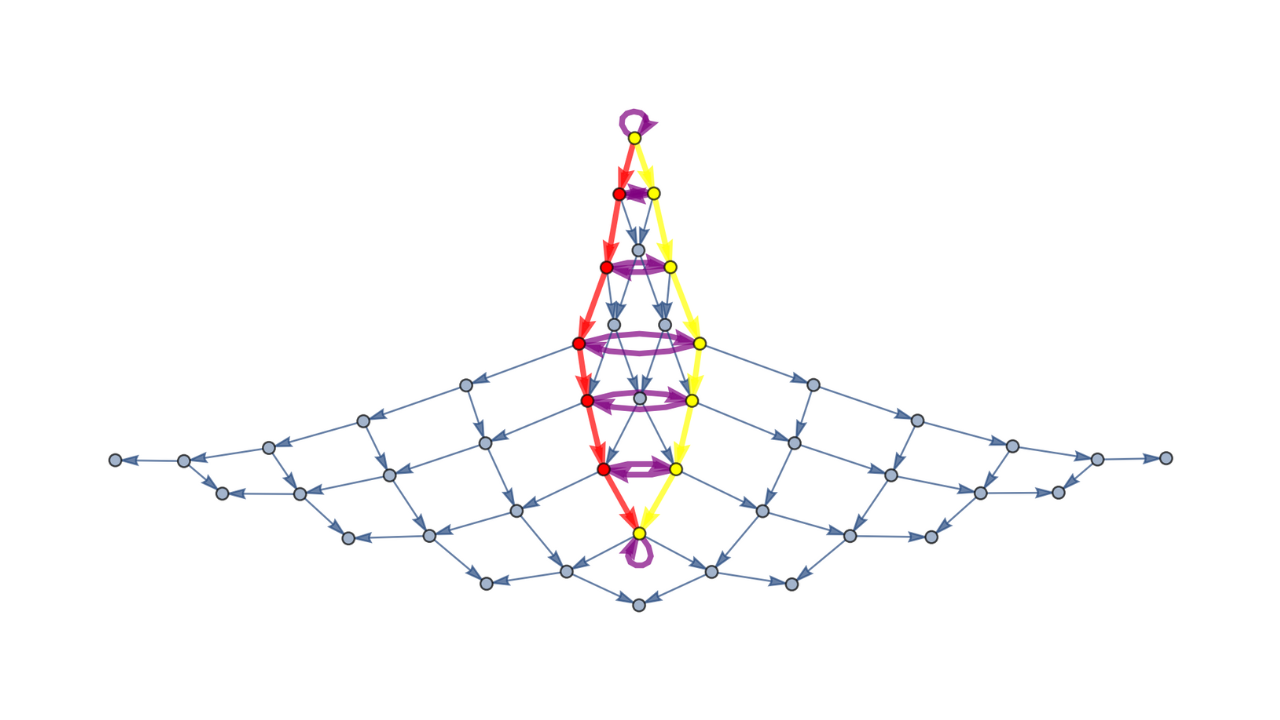
Homotopies in Multiway (Non-Deterministic) Rewriting Systems as n-Fold Categories
Xerxes D. Arsiwalla, Jonathan Gorard, Hatem Elshatlawy
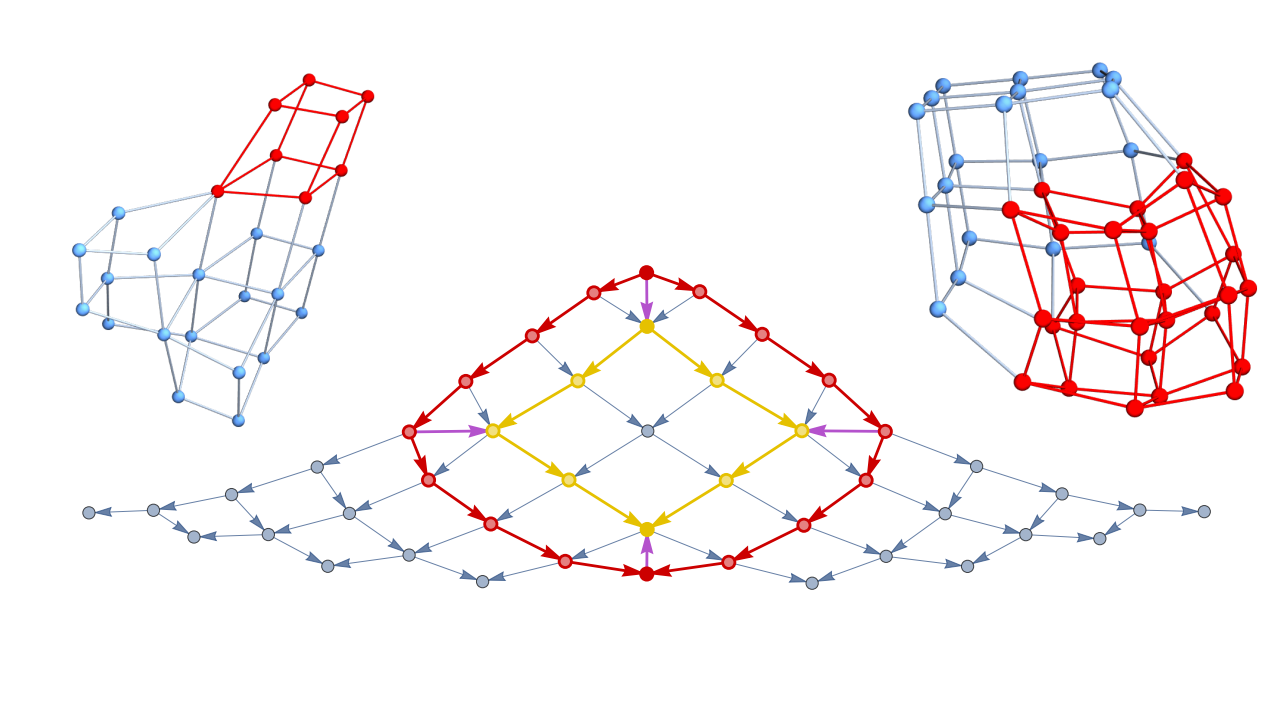
Pregeometric Spaces from Wolfram Model Rewriting Systems as Homotopy Types
Xerxes D. Arsiwalla, Jonathan Gorard
The study explores how spatial structures in physics can emerge from pregeometric combinatorial models governed by computational rules, using higher category theory and homotopy types.

Some Relativistic and Gravitational Properties of the Wolfram Model
Jonathan Gorard
The article shows that causal invariance in the Wolfram Model leads to discrete general and Lorentz covariance, introducing curvature concepts for hypergraphs related to the Ricci tensor and Einstein field equations

Algorithmic Causal Sets and the Wolfram Model
Jonathan Gorard
This study links causal set theory and the Wolfram model, showing hypergraph rewriting facilitates causal set evolution, infers conformal invariance, and derives the Benincasa-Dowker action from discrete Einstein-Hilbert action.

Hypergraph Discretization of the Cauchy Problem in General Relativity via Wolfram Model Evolution
Jonathan Gorard
This article introduces a numerical general relativity code using the Z4 formulation with hypergraph-based Cauchy data and adaptive mesh refinement, validating results against standard spacetimes and comparing with Wolfram model evolution.
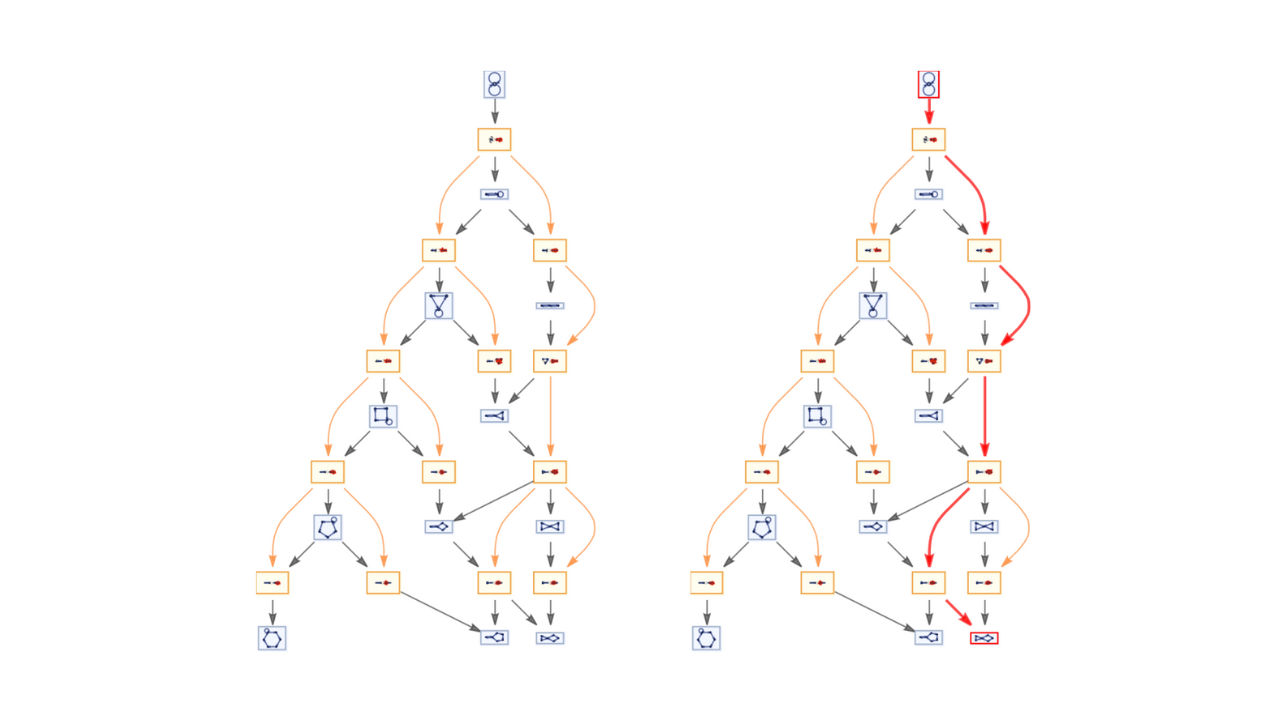
Fast Automated Reasoning over String Diagrams using Multiway Causal Structure
Jonathan Gorard, Manojna Namuduri, Xerxes D. Arsiwalla

ZX-Calculus and Extended Wolfram Model Systems II: Fast Diagrammatic Reasoning with an Application to Quantum Circuit Simplification
Jonathan Gorard, Manojna Namuduri, Xerxes D. Arsiwalla

ZX-Calculus and Extended Hypergraph Rewriting Systems I: A Multiway Approach to Categorical Quantum Information Theory
Jonathan Gorard, Manojna Namuduri, Xerxes D. Arsiwalla

