Causality, Observers & Computation: A New Approach to Fundamental Physics
This project led by the Wolfram Institute intends to advance some specific directions of the Wolfram Physics Project and the Wolfram Metamathematics Project revolving around the concepts of causality, discrete observers and generalized forms of computation. A common feature across areas of research in this project is the study and implementation of hypergraph rewrite systems. Additionally, this project aims to build bridges with existing areas of mathematics and computer science such as categorical rewriting theory, higher-order structures and graph computation.
This project was made possible through the support of Grant 63655 from the John Templeton Foundation. The opinions expressed in this publication are those of the author(s) and do not necessarily reflect the views of the John Templeton Foundation.
People
-

Stephen Wolfram
Project Leader
-

Carlos Zapata-Carratalá
Project Leader
-

Nicolas Behr
Université Cité (Paris)
-

Joshua A. Grochow
University of Colorado (Boulder)
-

Alexander Kolpakov
UATX (Austin)
Executive Overview
What is time? What divides the observer from the observed? Is reality fundamentally computational or mathematical? These questions are at the core of multiple frontiers of modern science, ranging from quantum physics and cosmology to consciousness studies and complexity. This project will address these questions from a parsimonious perspective, and investigate causality in hypergraph rewrite systems - an emerging research area at the intersection of mathematics, computer science and physics. Originating in this field, there have been early indications of a new paradigm that may transform how mathematical science is practiced fundamentally. This project aims to consolidate the first rigorous advancements to establish a new computational paradigm for fundamental science. The project will not only result in publications and events by which we communicate this new approach within the larger scientific community, but we will also create extensive computational functionality and training materials publicly available in the permanent project website and repositories. Ultimately, this project is positioned to capitalize on the technological progress of the last few decades, taking computation as a starting point, rather than a mere methodology. Not unlike inventions such as scripts, paper or the printing press, we believe that the computational framework put forward by this project will fundamentally transform how we approach mathematics and fundamental science in centuries to come.
Project Details
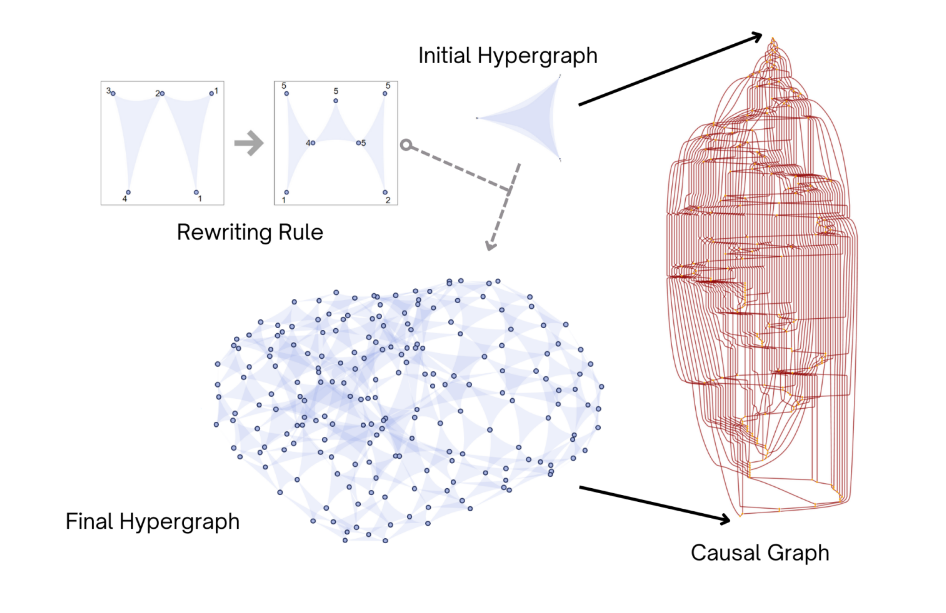
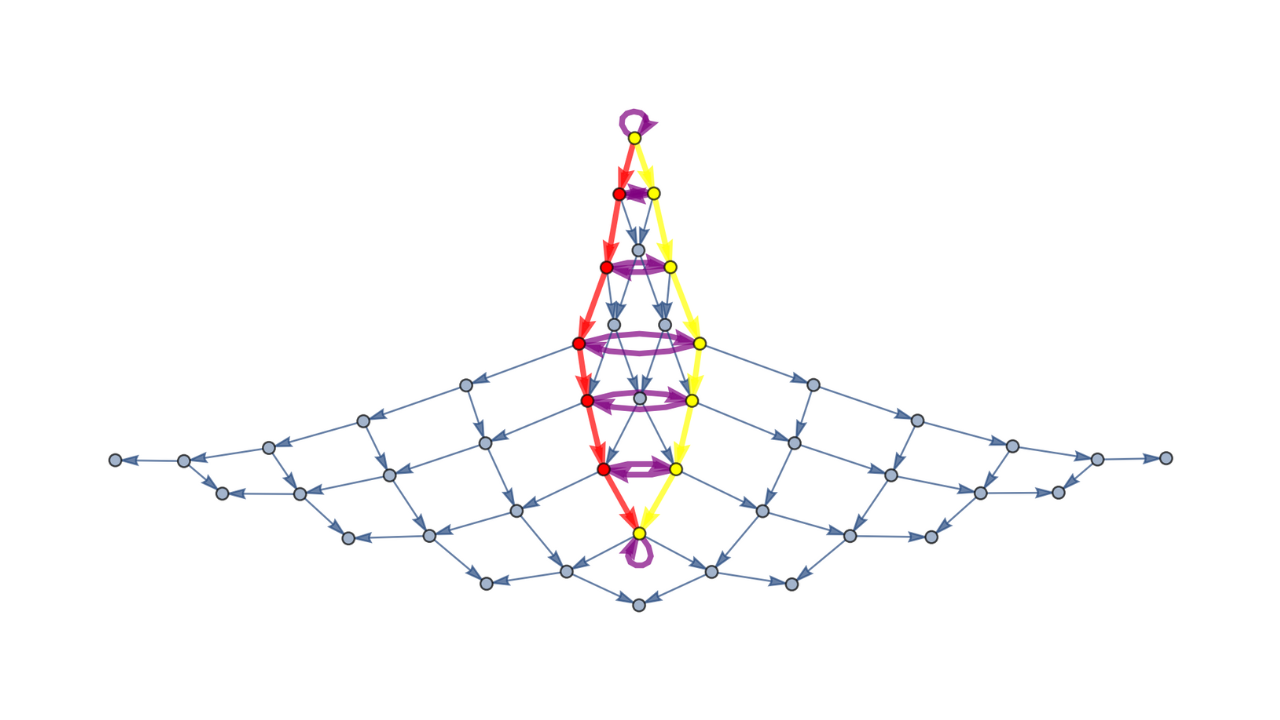
Causal Structure of Rewriting and Discrete Observers
The dependency of local rewrites in a hypergraph creates a causal structure analogous to those used in informational physics and causal set theory. Discrete observers are thus defined in direct analogy with relativistic observers in a Lorentzian manifold. To investigate:
Discrete analogue of the Principle of General Covariance.
Branching points and information entanglement.
Classical and quantum observers as discrete observers.
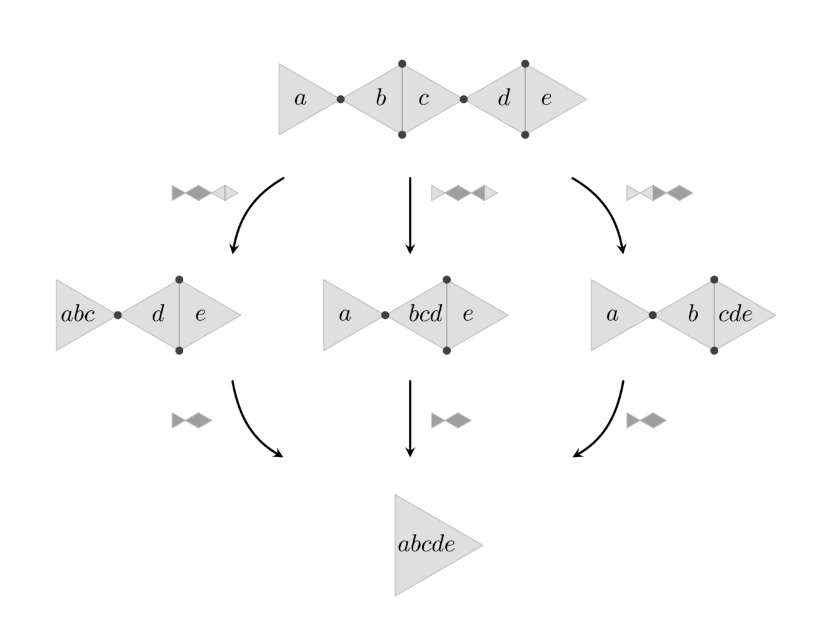
A New Kind of Computational Mathematics
Working with discrete structures requires a mathematical framework that allows for multi-scale, higher-order and partially-defined operations, i.e. generalizing ordinary notions in set theory and category theory. This is accomplished by using partial hypergraph rewriting algebras and tensor algebra. To investigate:
Generalized arity and higher-order sequential operations.
Algebraic axioms and confluence of diagrammatic rewrite systems.
Formal system emulation and computational invariance.
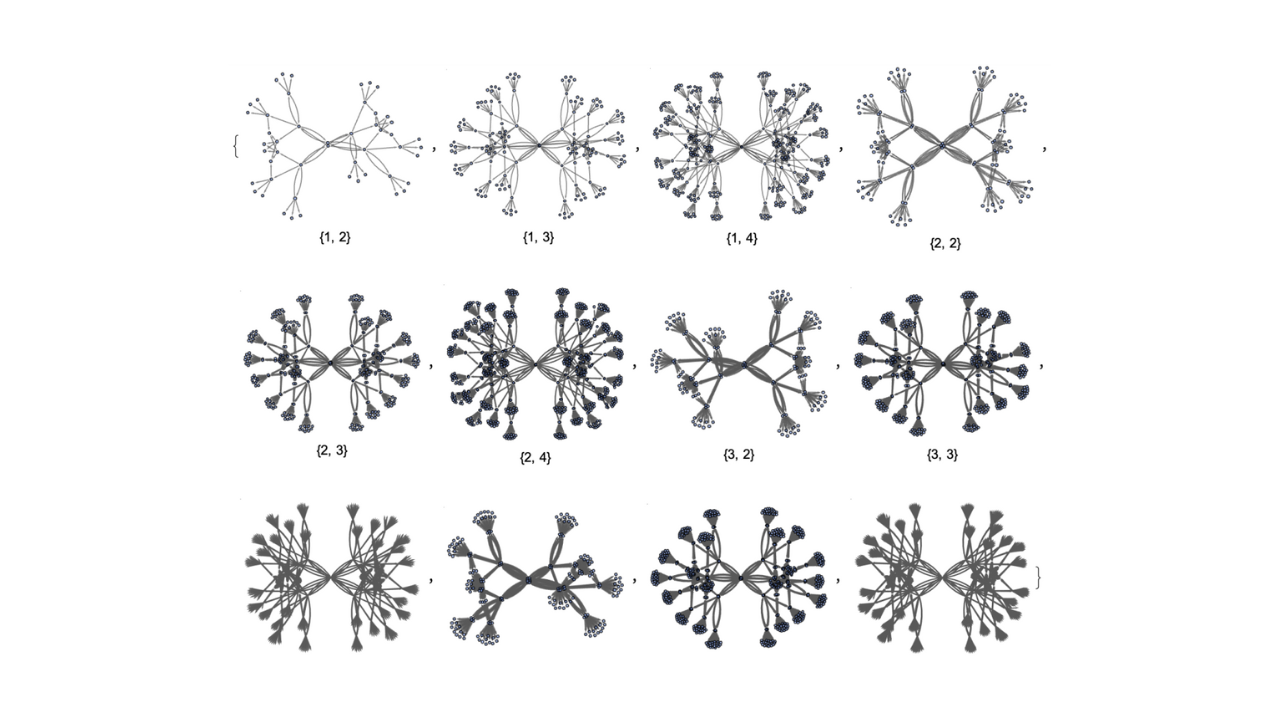
Hypergraphs as Discrete Models of Space
Hypergraphs are generalizations of simplicial complexes, which are well-known discretizations of continuous space; hence one can capture exotic geometries in a discrete form, e.g. generalized Lorentzian and Carrollian spacetimes. To investigate:
Formalization of discrete geometry in hypergraphs.
Taxonomy of discrete geometries from their generative rewriting processes.
Hypergraph-theoretic definitions of topological and geometric invariants.
Building on key results from each of the above, the project will then focus on the following open problems:
What are the discrete analogues of classical mechanics? What rewriting rules lead to Galilean relativity?
Is quantum entanglement the result of local rewriting ambiguity? Can the measurement problem by reduced to a coarse-graining argument in multi-scale hypergraph rewriting?
How do particular hypergraph rewrite rules affect the discrete spacetime structure they generate?
Can Einstein field equations be derived as large-cardinality limits of hypergraph rewriting systems?
Do gauge theories and QFTs emerge in a similar manner when considering branching phenomena at the rewriting level?
All this research will be conducted in connection with two important broader intellectual contexts: the general problem of quantum gravity and existing approaches to discrete spacetime, and the recent progress in mathematical multi-scale science, particularly with applications to machine learning and biology.
Relevant Resources
-
Stephen Wolfram: Complexity and the Fabric of Reality | Lex Fridman Podcast #234