Institute Output
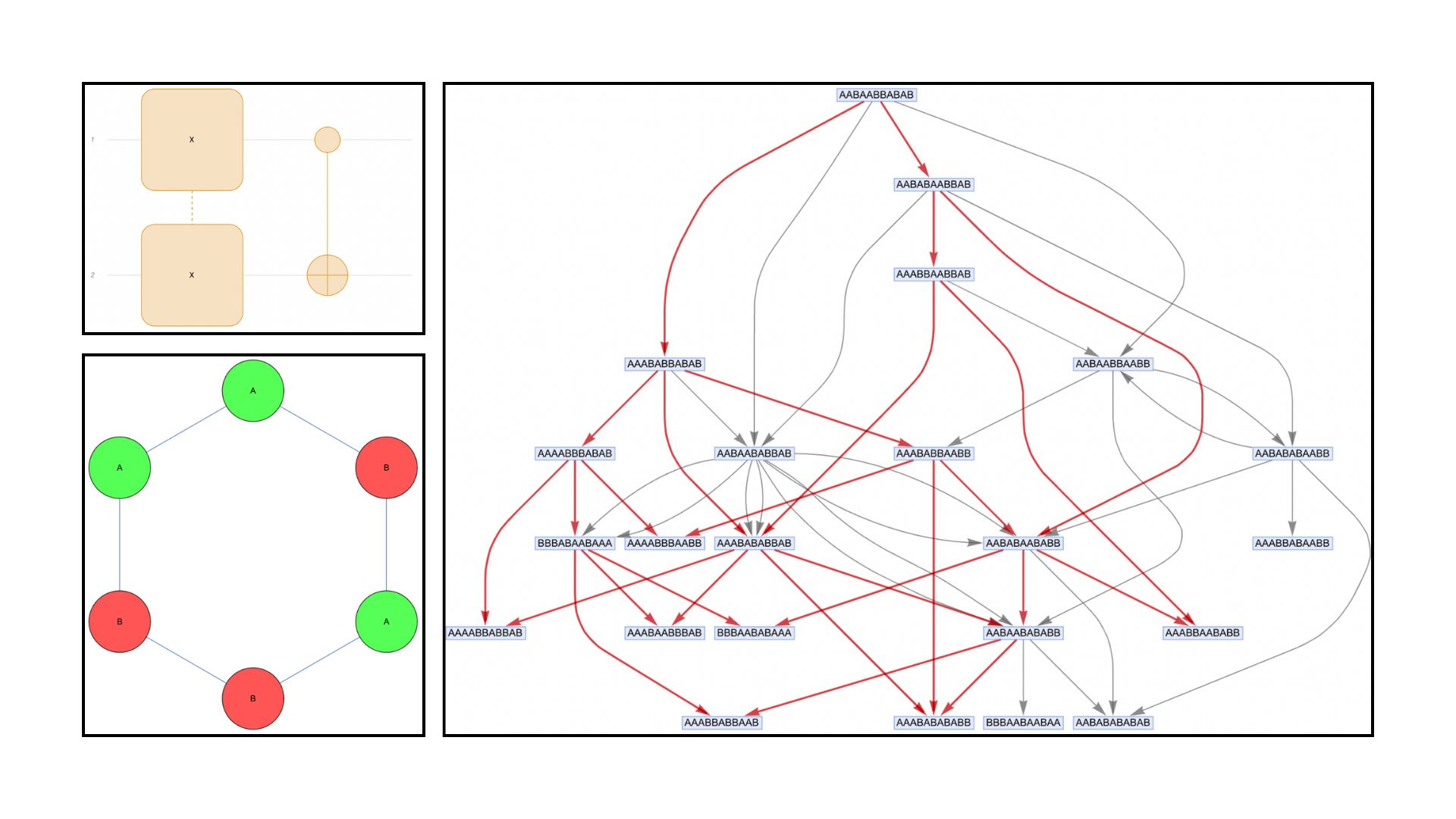
Quantum Operators From Wolfram Model Multiway Systems
Furkan Semih Dündar, Xerxes D. Arsiwalla, Hatem Elshatlawy
Using Wolfram Model multiway rewriting systems we have found that by using multiway systems one can construct representations of quantum circuits, showing that one can encode the Hadamard gate, the π/8 gate and the CNOT using multiway rewriting systems. This suggests the possibility of universal quantum computation using multiway rewriting.
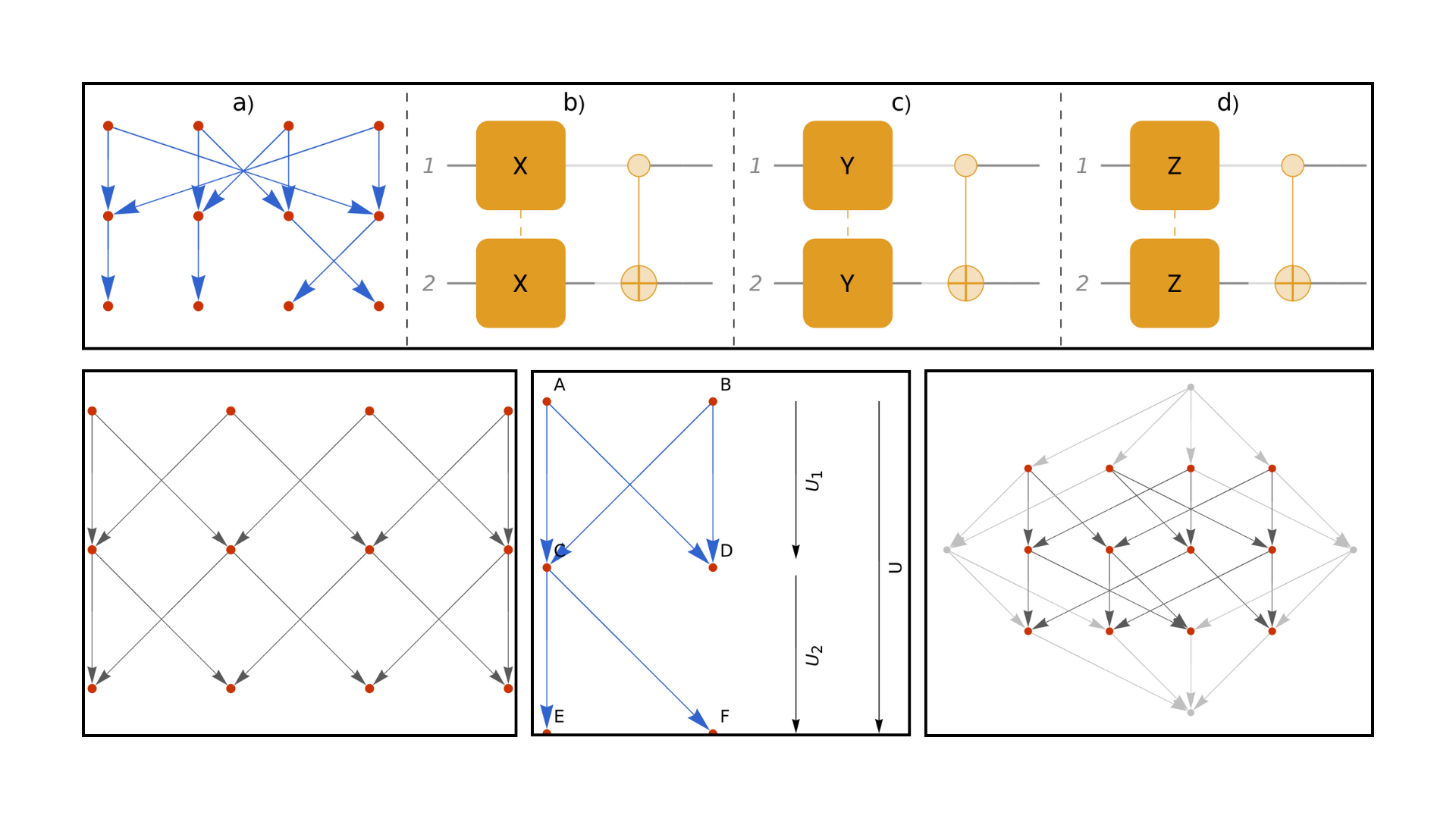
Quantum Gates from Wolfram Model Multiway Rewriting Systems
Furkan Semih Dündar, Xerxes D. Arsiwalla, Hatem Elshatlawy
We show how representations of finite-dimensional quantum operators can be constructed using nondeterministic rewriting systems. In particular, we investigate Wolfram model multiway rewriting systems based on string substitutions.

Quantum Gravity and Computation: Information, Pregeometry, and Digital Physics
Dean Rickles, Xerxes D. Arsiwalla, Hatem Elshatlawy
This volume argues that concepts from the theory of computation—including information theory, formal languages, and discrete structures—might provide novel paths towards a solution to the problem of quantum gravity. By combining elements of physics with computer science and mathematics, the volume proposes to transform the foundations of spacetime physics and bring it into the digital age.

Upper Bounds on the Chromatic Index of Linear Hypergraphs
Thomas Murff, Xerxes D. Arsiwalla
This work studies upper bounds on the chromatic index of linear, loopless hypergraphs. The first bound is derived using a color-preserving group acting on a properly and minimally edge-colored hypergraph, where the group’s orbits create a finer partition of the coloring. This provides an upper bound on the chromatic index. The following results examine combinatorial properties of hypergraph coloring and outline a possible approach to the Berge–Füredi conjecture, linking the chromatic index to the maximum degree of the associated graph plus one. Three sufficient conditions are also identified for the conjecture to hold, involving the Helly property for hypergraphs.
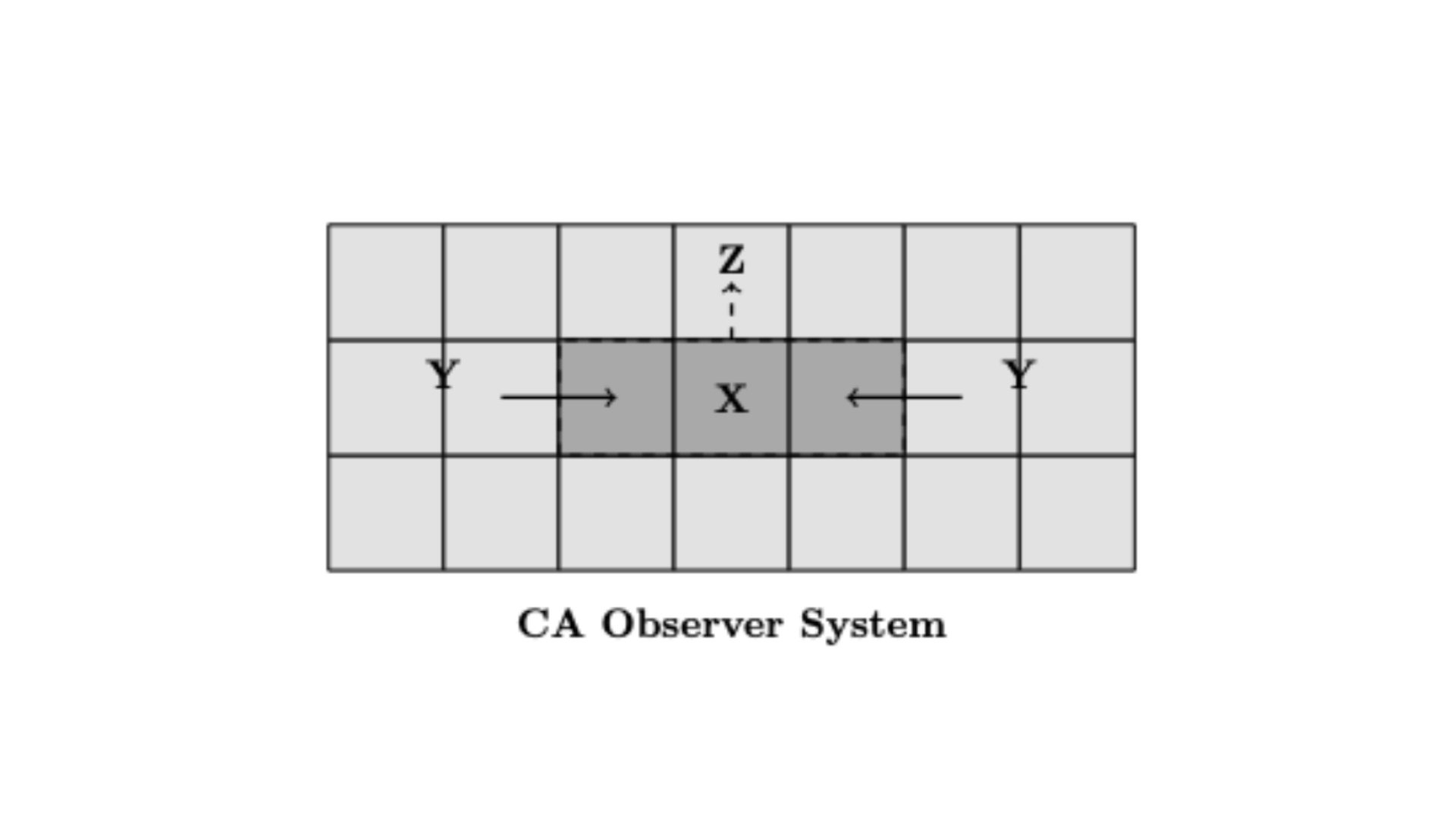
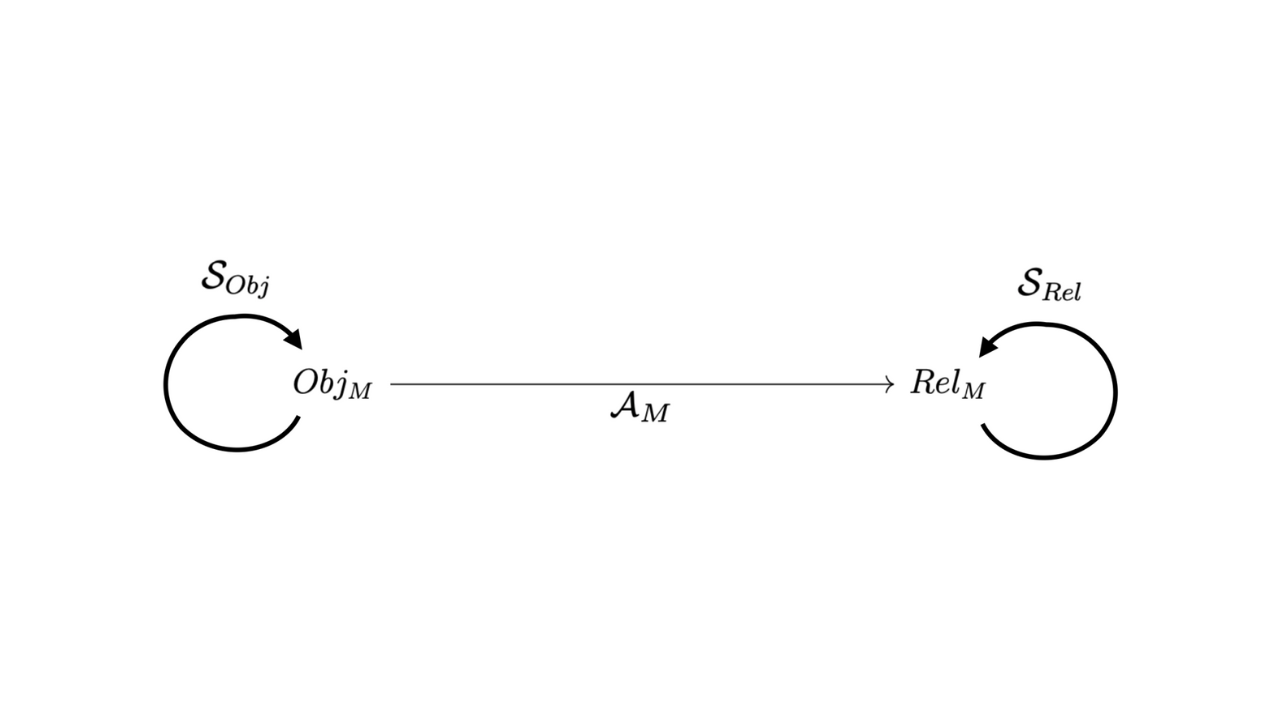
Towards a Generalized Theory of Observers
Hatem Elshatlawy, Xerxes Arsiwalla
A proposal of a formal framework for understanding and unifying the concept of observers across physics, computer science, philosophy, and related fields.

Non-Equilibrium Dynamics of Hard Spheres in the Fluid, Crystalline, and Glassy Regimes
Xerxes D. Arsiwalla, Matthew Kafker
An investigation of the response of a system of hard spheres to two classes of perturbations over a range of densities spanning the fluid, crystalline, and glassy regimes within a molecular dynamics framework.

Preons, Braid Topology, and Representations of Fundamental Particles
David Chester, Xerxes D. Arsiwalla, Louis H. Kauffman
Braided ribbon topology for representing Standard Model fermions and their interactions
Qualia and the Formal Structure of Meaning
Xerxes D. Arsiwalla
This work explores the hypothesis that subjectively attributed meaning constitutes the phenomenal content of conscious experience. This form of subjective meaning manifests as an intrinsic and non-representational character of qualia.

An Invitation to Higher Arity Science
Carlos Zapata-Carratalá, Xerxes D. Arsiwalla
Exploration of a wide range of higher-order phenomena across multiple disciplines and the preliminary application of hypergraph and hypermatrix methods.

On the operator origins of classical and quantum wave functions
Xerxes D. Arsiwalla, David Chester, Louis H. Kauffman
We investigate operator algebraic origins of the classical Koopman–von Neumann wave function $\psi_{KvN}$ as well as the quantum-mechanical one $\psi_{QM}$. In particular $\psi_{KvN}$, and $\psi_{QM}$ are both consequences of this pre-quantum formalism. What this suggests is that neither the Schrödinger equation nor the quantum wave function are fundamental structures.
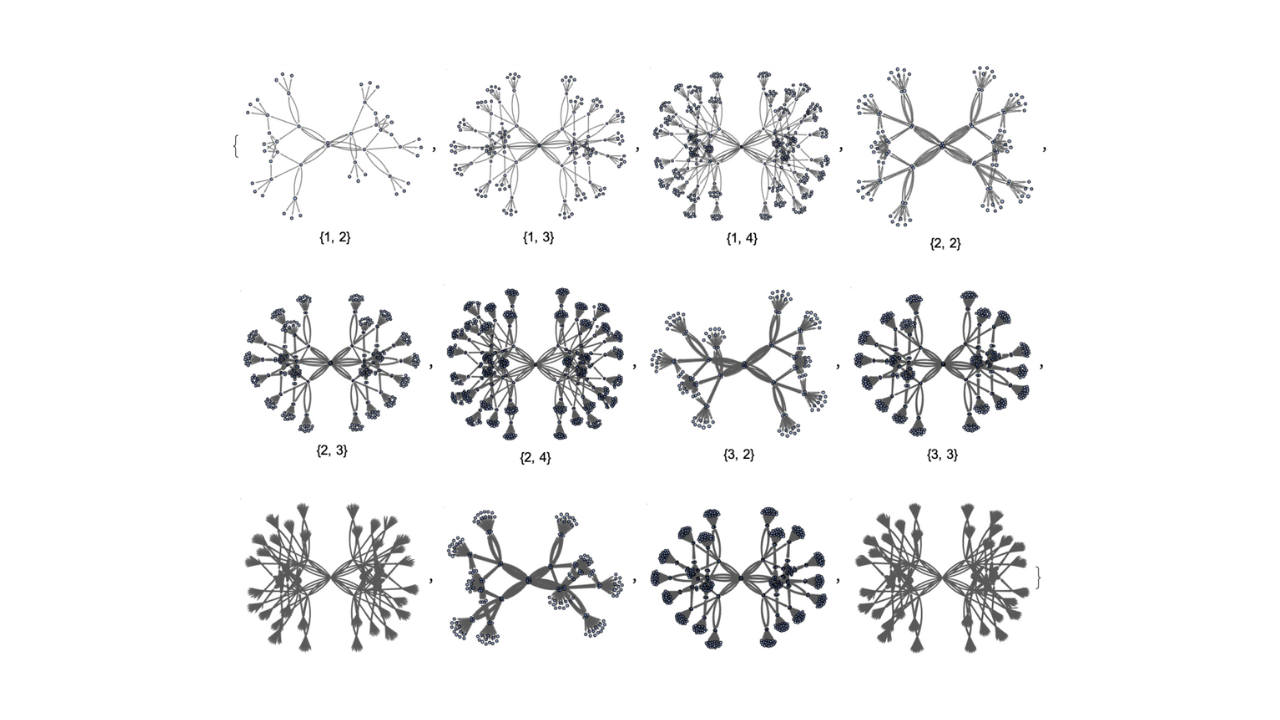
Ruliology: Linking Computation, Observers and Physical Law
Dean Rickles, Hatem Elshatlawy, Xerxes D. Arsiwalla
Physical laws arise from the sampling of the Ruliad by observers (including us). This naturally leads to several conceptual issues, such as what kind of object is the Ruliad? What is the nature of the observers carrying out the sampling, and how do they relate to the Ruliad itself? What is the precise nature of the sampling? This paper provides a philosophical examination of these questions, and other related foundational issues, including the identification of a limitation that must face any attempt to describe or model reality in such a way that the modeller-observers are included.

Hypermatrix Algebra and Irreducible Arity in Higher-Order Systems: Concepts and Perspectives
Carlos Zapata-Carratalá, Maximilian Schich, Taliesin Beynon, Xerxes D. Arsiwalla
Hypergraph and hypermatrix methods are applied to detect irreducible interactions in higher-order systems.

A Cosine Rule-Based Discrete Sectional Curvature for Graphs
Xerxes D. Arsiwalla, J.F. Du Plessis
How does one generalize differential geometric constructs such as curvature of a manifold to the discrete world of graphs and other combinatorial structures? This problem carries significant importance for analyzing models of discrete spacetime in quantum gravity; inferring network geometry in network science; and manifold learning in data science. The key contribution of this paper is to introduce and validate a new estimator of discrete sectional curvature for random graphs with low metric-distortion.

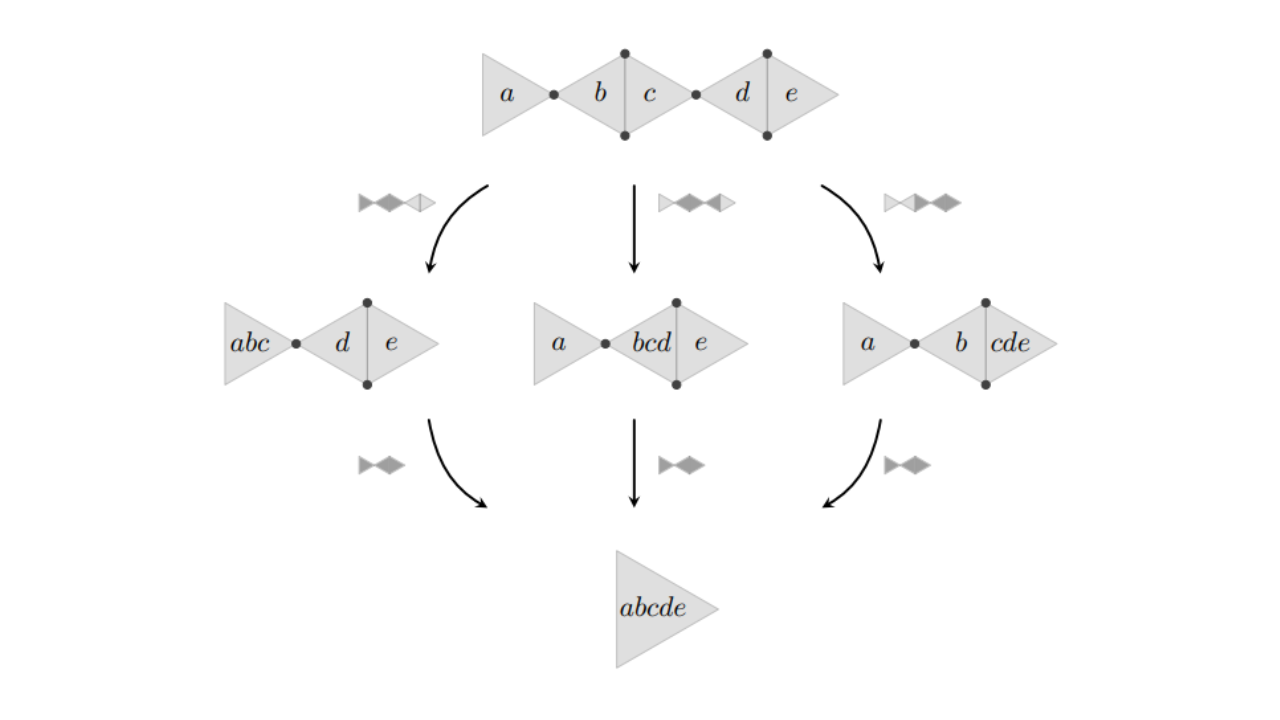
Heaps of Fish: arrays, generalized associativity and heapoids
Carlos Zapata-Carratala, Xerxes D. Arsiwalla, Taliesin Beynon
In this paper we investigate a ternary generalization of associativity by defining a diagrammatic calculus of hypergraphs that extends the usual notions of tensor networks, categories and relational algebras. In doing so we rediscover the ternary structures known as heaps and are able to give a more comprehensive treatment of their mergence in the context of dagger categories and their generalizations.
Diagrammatic calculus and generalized associativity for higher-arity tensor operations
Carlos Zapata-Carratalá, Xerxes D. Arsiwalla, Taliesin Beynon
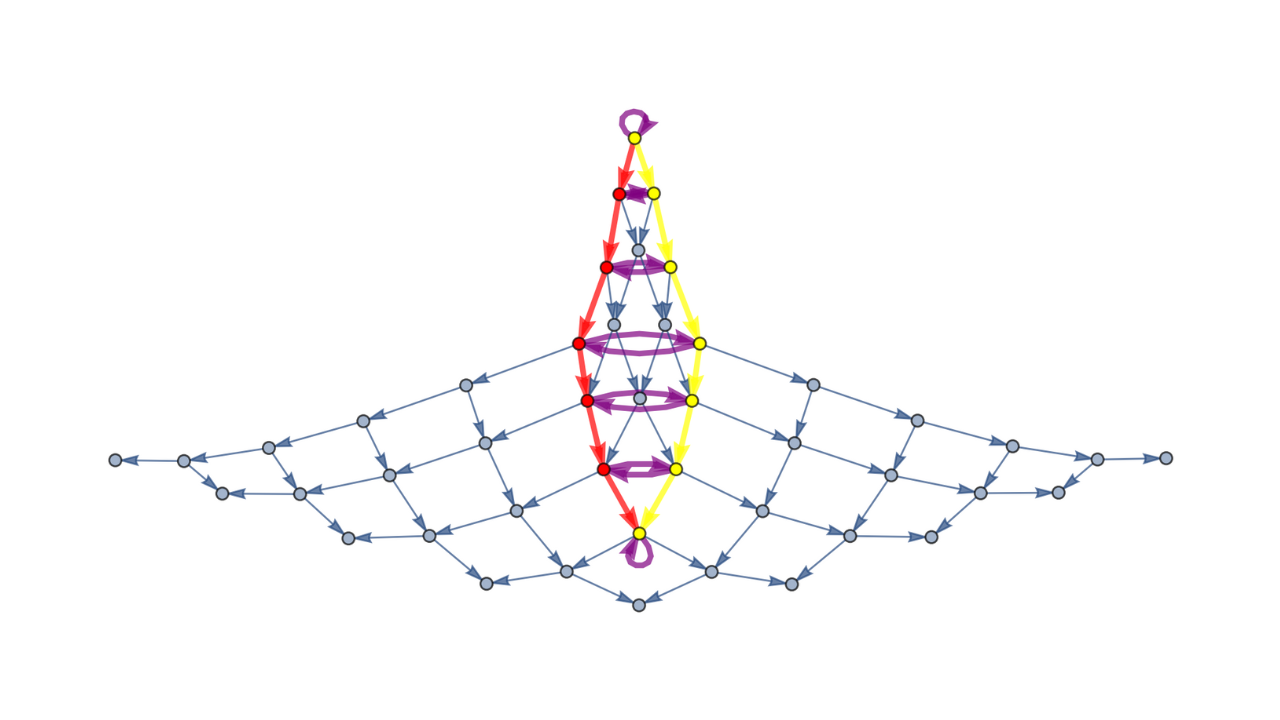
Homotopies in Multiway (Non-Deterministic) Rewriting Systems as n-Fold Categories
Xerxes D. Arsiwalla, Jonathan Gorard, Hatem Elshatlawy
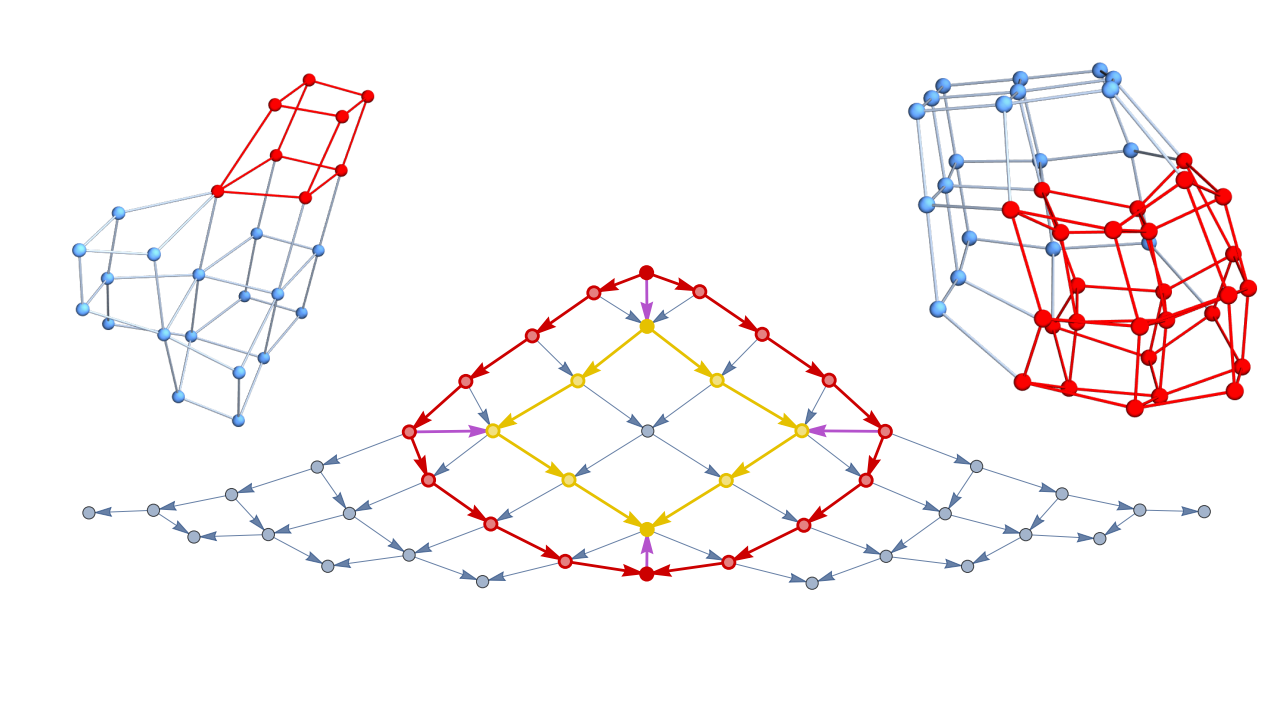
Pregeometric Spaces from Wolfram Model Rewriting Systems as Homotopy Types
Xerxes D. Arsiwalla, Jonathan Gorard
The study explores how spatial structures in physics can emerge from pregeometric combinatorial models governed by computational rules, using higher category theory and homotopy types.
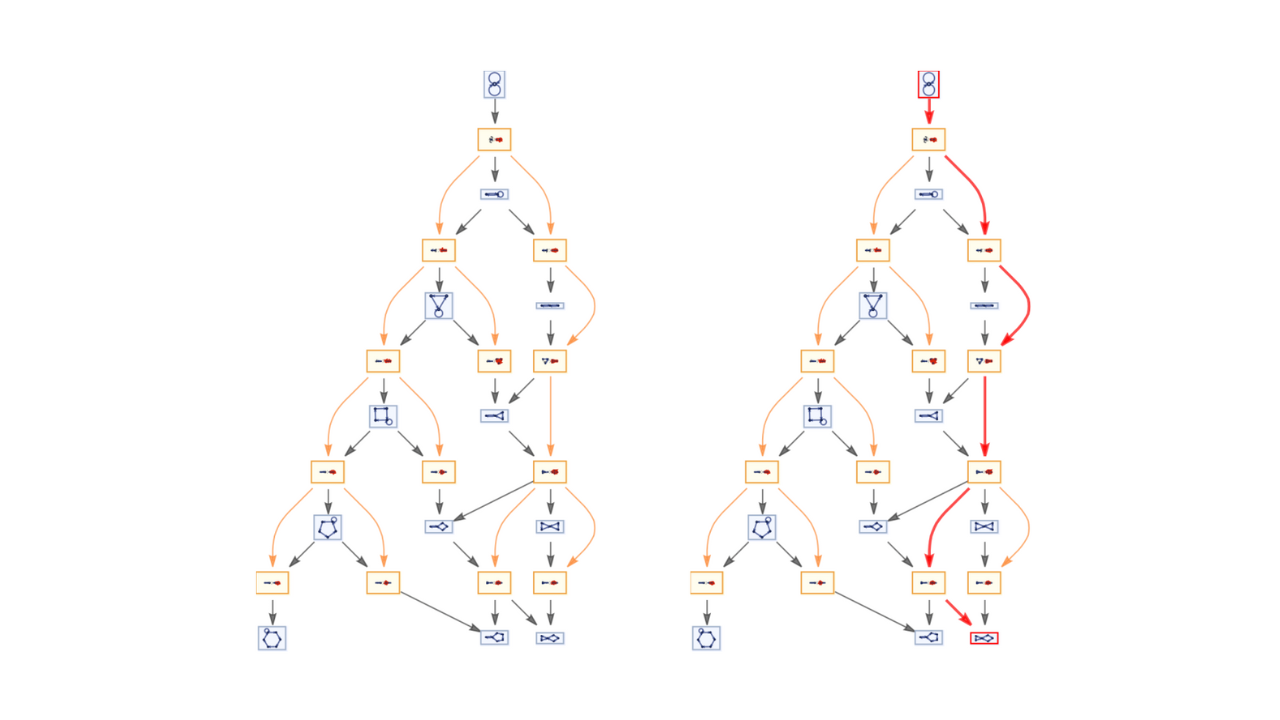
Fast Automated Reasoning over String Diagrams using Multiway Causal Structure
Jonathan Gorard, Manojna Namuduri, Xerxes D. Arsiwalla

ZX-Calculus and Extended Wolfram Model Systems II: Fast Diagrammatic Reasoning with an Application to Quantum Circuit Simplification
Jonathan Gorard, Manojna Namuduri, Xerxes D. Arsiwalla

ZX-Calculus and Extended Hypergraph Rewriting Systems I: A Multiway Approach to Categorical Quantum Information Theory
Jonathan Gorard, Manojna Namuduri, Xerxes D. Arsiwalla
