Institute Output
Hypermatrix Algebra and Irreducible Arity in Higher-Order Systems: Concepts and Perspectives
Carlos Zapata-Carratalá, Maximilian Schich, Taliesin Beynon, Xerxes D. Arsiwalla
Hypergraph and hypermatrix methods are applied to detect irreducible interactions in higher-order systems.
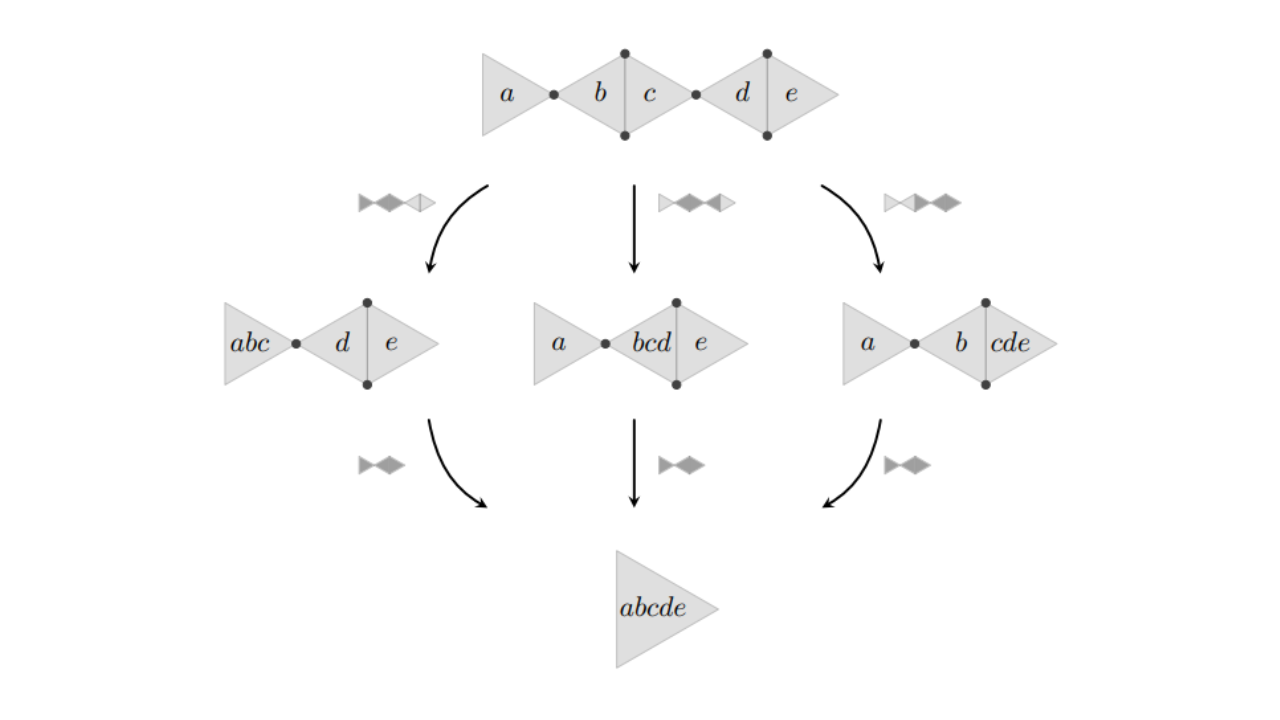
Diagrammatic calculus and generalized associativity for higher-arity tensor operations
Carlos Zapata-Carratalá, Xerxes D. Arsiwalla, Taliesin Beynon