Institute Output

Computational Foundations for the Second Law of Thermodynamics
Stephen Wolfram
Entropy increases. Mechanical work irreversibly turns into heat. The Second Law of thermodynamics is considered one of the great general principles of physical science. But 150 years after it was first introduced, there’s still something deeply mysterious about the Second Law. It almost seems like it’s going to be “provably true”. But one never quite gets there; it always seems to need something extra. Sometimes textbooks will gloss over everything; sometimes they’ll give some kind of “common-sense-but-outside-of-physics argument”. But the mystery of the Second Law has never gone away.
A 50-Year Quest: My Personal Journey with the Second Law of Thermodynamics
Stephen Wolfram
The wonder and magic of the Second Law is still there. But now I’m able to see it in a much broader context, and to realize that it’s not just a law about thermodynamics and heat, but instead a window into a very general computational phenomenon.

How Did We Get Here? The Tangled History of the Second Law of Thermodynamics
Stephen Wolfram
As I’ve explained elsewhere, I think I now finally understand the Second Law of thermodynamics. But it’s a new understanding, and to get to it I’ve had to overcome a certain amount of conventional wisdom about the Second Law that I at least have long taken for granted. And to check myself I’ve been keen to know just where this conventional wisdom came from, how it’s been validated, and what might have made it go astray.

Axiomatic Quantum Field Theory in Discrete Spacetime via Multiway Causal Structure: The Case of Entanglement Entropies
Jonathan Gorard, Julia Dannemann-Freitag
This research examines a covariant approach to entanglement entropy in discrete quantum gravity, comparing causal set and Wolfram model frameworks to reveal a monotonic relationship.

Alien Intelligence and the Concept of Technology
Stephen Wolfram
“We’re going to launch lots of tiny spacecraft into interstellar space, have them discover alien intelligence, then bring back its technology to advance human technology by a million years”.
But as I thought about it, I realized that beyond the “absurdly extreme moonshot” character of this pitch, there’s some science that I’ve done that makes it clear that it’s also fundamentally philosophically confused. The nature of the confusion is interesting, however, and untangling it will give us an opportunity to illuminate some deep features of both intelligence and technology—and in the end suggest a way to think about the long-term trajectory of the very concept of technology and its relation to our universe.

Games and Puzzles as Multicomputational Systems
Stephen Wolfram
Multicomputation is one of the core ideas of the Wolfram Physics Project—and in particular is at the heart of our emerging understanding of quantum mechanics. But how can one get an intuition for what is initially the rather abstract idea of multicomputation? A good approach, I believe, is to see it in action in familiar systems and situations. And I explore here what seems like a particularly good example: games and puzzles.
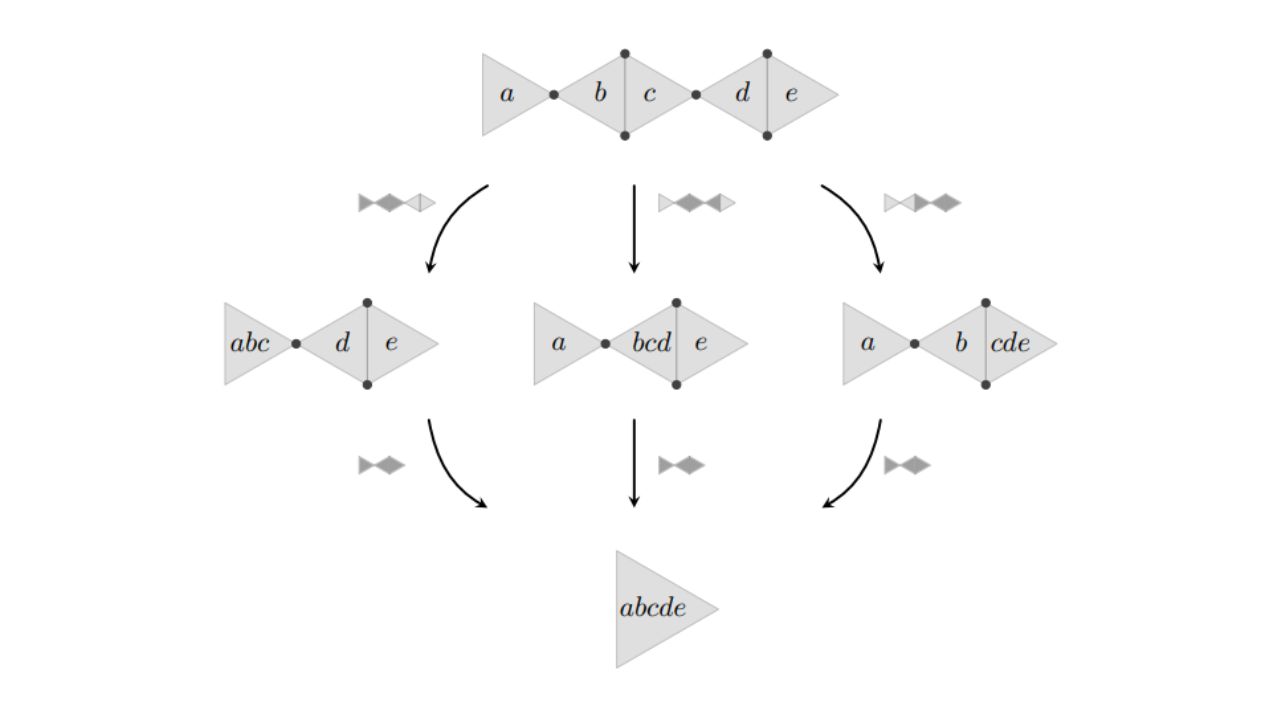
Diagrammatic calculus and generalized associativity for higher-arity tensor operations
Carlos Zapata-Carratalá, Xerxes D. Arsiwalla, Taliesin Beynon

We’ve Got a Science Opportunity Overload: It’s Time to Launch the Wolfram Institute!
Stephen Wolfram
We’re in the midst of a major “science opportunity overload”. And to be good stewards of the ideas and their potential we’ve got to scale things up. I’ve had lots of experience over decades in making big projects happen. And now it’s time to take that experience and define a new structure to move forward the amazing science opportunity we find ourselves with. And I think that leaves us no choice: we’ve got to launch the Wolfram Institute, and now!

On the Concept of Motion
Stephen Wolfram
It seems like the kind of question that might have been hotly debated by ancient philosophers, but would have been settled long ago: how is it that things can move? And indeed with the view of physical space that’s been almost universally adopted for the past two thousand years it’s basically a non-question. As crystallized by the likes of Euclid it’s been assumed that space is ultimately just a kind of “geometrical background” into which any physical thing can be put—and then moved around.

The Physicalization of Metamathematics and Its Implications for the Foundations of Mathematics
Stephen Wolfram
One of the many surprising (and to me, unexpected) implications of our Physics Project is its suggestion of a very deep correspondence between the foundations of physics and mathematics. We might have imagined that physics would have certain laws, and mathematics would have certain theories, and that while they might be historically related, there wouldn’t be any fundamental formal correspondence between them.
But what our Physics Project suggests is that underneath everything we physically experience there is a single very general abstract structure—that we call the ruliad—and that our physical laws arise in an inexorable way from the particular samples we take of this structure.
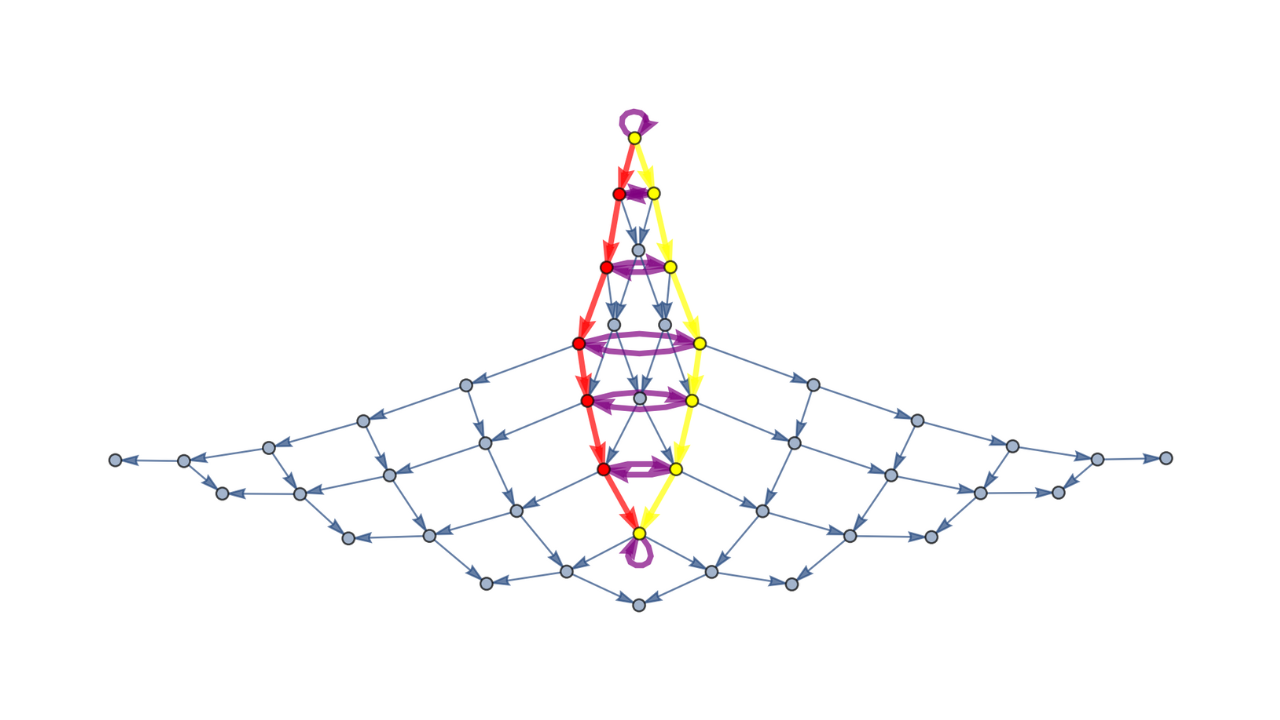
Homotopies in Multiway (Non-Deterministic) Rewriting Systems as n-Fold Categories
Xerxes D. Arsiwalla, Jonathan Gorard, Hatem Elshatlawy
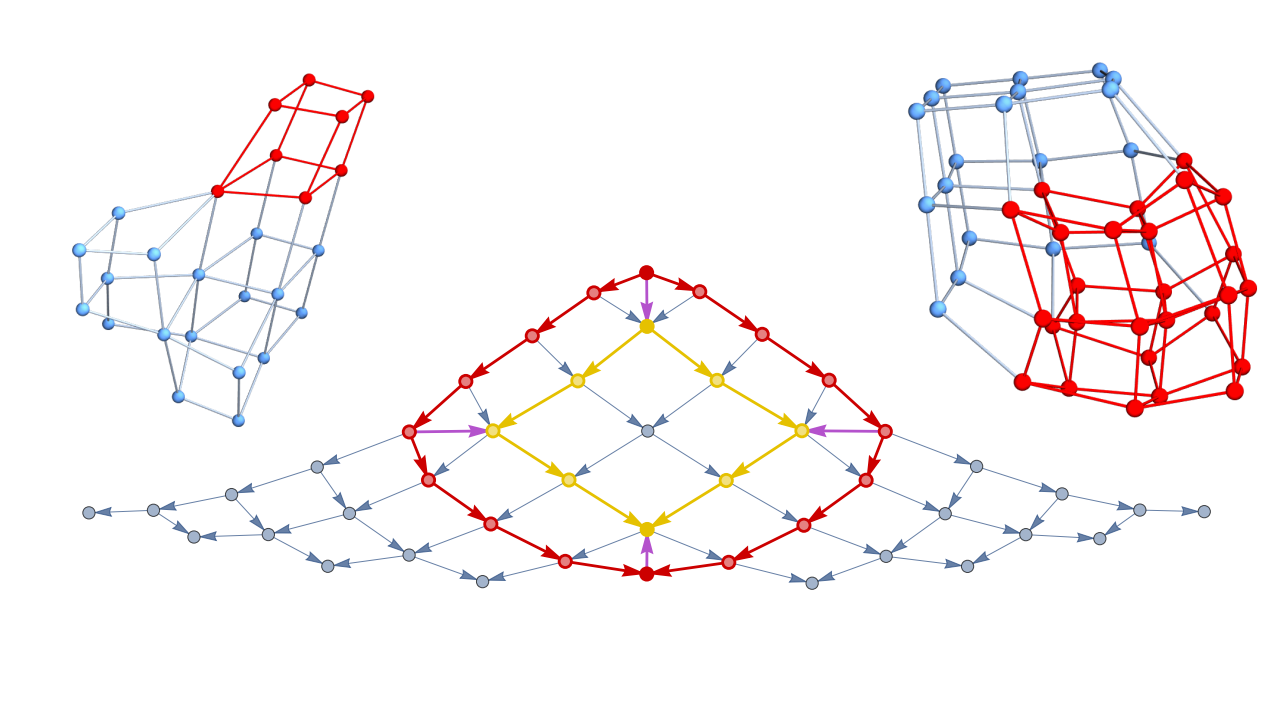
Pregeometric Spaces from Wolfram Model Rewriting Systems as Homotopy Types
Xerxes D. Arsiwalla, Jonathan Gorard
The study explores how spatial structures in physics can emerge from pregeometric combinatorial models governed by computational rules, using higher category theory and homotopy types.

The Concept of the Ruliad
Stephen Wolfram
I call it the ruliad. Think of it as the entangled limit of everything that is computationally possible: the result of following all possible computational rules in all possible ways. It’s yet another surprising construct that’s arisen from our Physics Project. And it’s one that I think has extremely deep implications—both in science and beyond.

Some Relativistic and Gravitational Properties of the Wolfram Model
Jonathan Gorard
The article shows that causal invariance in the Wolfram Model leads to discrete general and Lorentz covariance, introducing curvature concepts for hypergraphs related to the Ricci tensor and Einstein field equations

Algorithmic Causal Sets and the Wolfram Model
Jonathan Gorard
This study links causal set theory and the Wolfram model, showing hypergraph rewriting facilitates causal set evolution, infers conformal invariance, and derives the Benincasa-Dowker action from discrete Einstein-Hilbert action.

Hypergraph Discretization of the Cauchy Problem in General Relativity via Wolfram Model Evolution
Jonathan Gorard
This article introduces a numerical general relativity code using the Z4 formulation with hypergraph-based Cauchy data and adaptive mesh refinement, validating results against standard spacetimes and comparing with Wolfram model evolution.

Multicomputation with Numbers: The Case of Simple Multiway Systems
Stephen Wolfram
Multicomputation is an important new paradigm, but one that can be quite difficult to understand. Here my goal is to discuss a minimal example: multiway systems based on numbers. Many general multicomputational phenomena will show up here in simple forms (though others will not). And the involvement of numbers will often allow us to make immediate use of traditional mathematical methods.

Charting a Course for “Complexity”: Metamodeling, Ruliology and More
Stephen Wolfram
For me the story began nearly 50 years ago—with what I saw as a great and fundamental mystery of science. We see all sorts of complexity in nature and elsewhere. But where does it come from? How is it made? There are so many examples. Snowflakes. Galaxies. Lifeforms. Turbulence. Do they all work differently? Or is there some common underlying cause? Some essential “phenomenon of complexity”?

Multicomputation: A Fourth Paradigm for Theoretical Science
Stephen Wolfram
One might have thought it was already exciting enough for our Physics Project to be showing a path to a fundamental theory of physics and a fundamental description of how our physical universe works. But what I’ve increasingly been realizing is that actually it’s showing us something even bigger and deeper: a whole fundamentally new paradigm for making models and in general for doing theoretical science. And I fully expect that this new paradigm will give us ways to address a remarkable range of longstanding central problems in all sorts of areas of science—as well as suggesting whole new areas and new directions to pursue.

How Inevitable Is the Concept of Numbers?
Stephen Wolfram
The aliens arrive in a starship. Surely, one might think, to have all that technology they must have the idea of numbers. Or maybe one finds an uncontacted tribe deep in the jungle. Surely they too must have the idea of numbers. To us numbers seem so natural—and “obvious”—that it’s hard to imagine everyone wouldn’t have them. But if one digs a little deeper, it’s not so clear.
